Essential Nodes And Essential Branches

What is an Essential Node?

A node is defined as a point where two or more circuit elements are connected. An essential node is a particular type of node where three or more elements are connected. An essential node is a useful node to consider in circuit analysis.

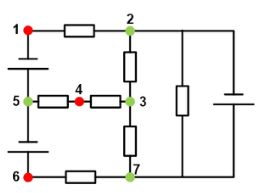
For example, in the below circuit, there is a total of seven nodes. Out of these seven nodes, there are four essential nodes that have been marked in green. The remaining three regular nodes have been marked in red.

What is an Essential Branch?

A branch is defined as a path that connects two or more nodes. An essential branch is a particular type of branch that connects essential nodes without passing an essential node.

That is to say that while an essential branch may pass through a regular node, it may not pass through an essential node. If this sounds confusing, take a look at the example below.

The circuit diagram below contains seven essential branches (B1 to B7).

Notice that B3 is an essential branch and that it passes through the non-essential node 4 (see prior diagram for node labeling).

Whereas the essential branches B4 and B5 are distinct essential branches. An essential branch does not exist between the top node (node 2 in the prior diagram) and the bottom node (node 7 in the prior diagram), because there exists an essential node in between these nodes (node 3 in the prior diagram).

Hence node 3, an essential node, “breaks up” the larger branch into two essential branches.

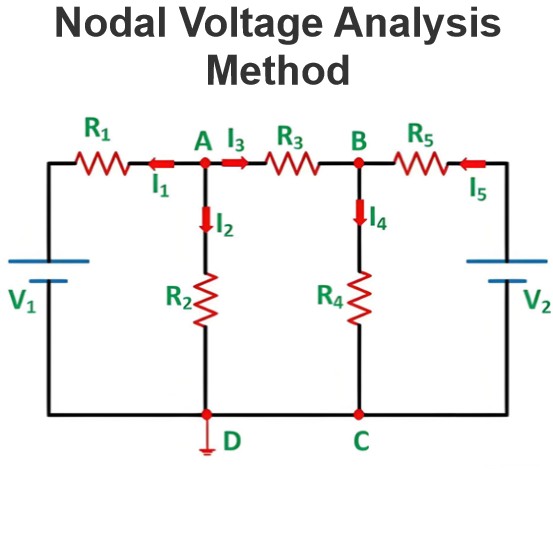
Essential Node Example

Essential nodes are very useful in circuit analysis. In nodal analysis, we can use only essential nodes to solve the circuit.

Let’s understand the impotence of essential nodes in circuit analysis with an example.

In this example, we will solve a circuit using the nodal analysis method. And in this method, we use only essential nodes.

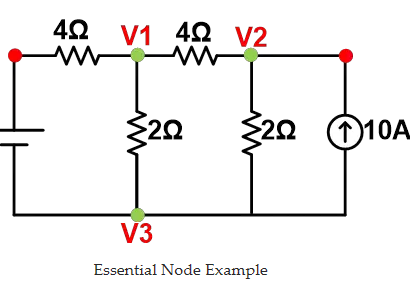
But for simple calculation, the essential node that is connected with a greater number of branches is chosen. And here, node V3 is a reference node.

n = the number of essential nodes in a circuit

Hence, the number of equations needed to solve this circuit is n-1=2.

At node-V1;

At node V2;

By solving these two equations, we can find the value of node voltages V1 and V.

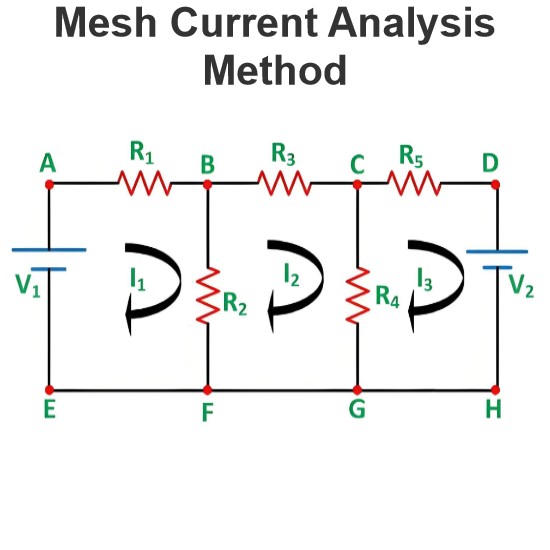
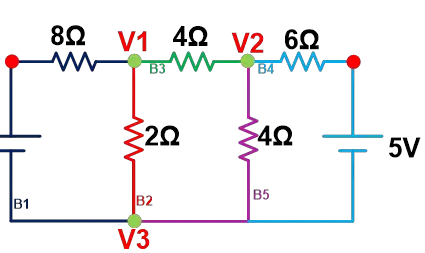
Essential Branch Example

Essential branches are useful in mesh analysis. See the circuit diagram below for a simple example.

Here:

• The total number of branches is 7

• The total number of essential branches is 5 (B1 to B5)

• The total number of essential nodes is 3 (V1 to V3)

Hence, the number of equations we need to solve this circuit is b-(n-1).

Here, for this example, the total number of equations required to solve this circuit is 3.

So, we apply KVL to each loop.

Loop-1

Loop-2

Loop-3

By solving these equations, we get the values of;

From the above values, we can find other circuit parameters like power offered by a voltage source, the current flowing through and the voltage across each element, etc.

Source: Electrical4u.

Statement: Respect the original, good articles worth sharing, if there is infringement please contact delete.