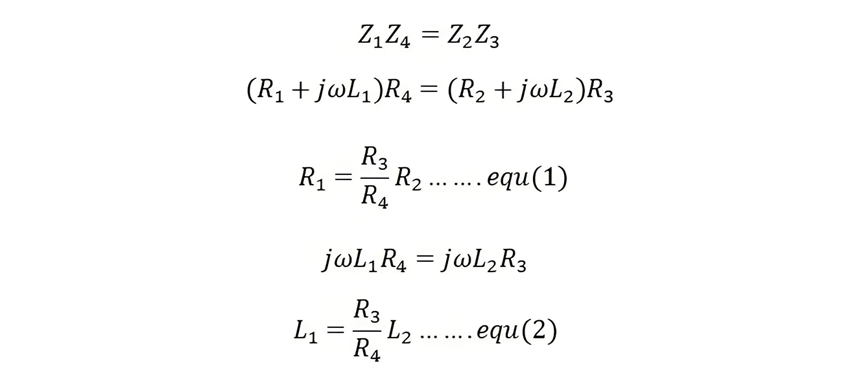Definition of AC Bridge
An AC bridge is a specialized electrical instrument used for the precise measurement of unknown electrical parameters such as resistance, inductance, and capacitance. Renowned for its convenience and accuracy, the AC bridge plays a crucial role in various electrical engineering applications.
Construction and Working Principle
The construction of an AC bridge is relatively straightforward. It comprises four arms, an AC supply source, and a balance detector. The four arms of the bridge are typically configured with a combination of resistors, inductors, capacitors, or a mixture of these components. The AC supply source provides the necessary alternating - current excitation to the bridge circuit.
The operation of the AC bridge is based on the principle of impedance balance. When the bridge is in a balanced state, the ratio of the impedances in the two pairs of opposite arms of the bridge is equal. This balance condition results in zero voltage across the balance detector, often referred to as a null detector. By measuring the known components in the bridge arms and using the relationship between the impedances at the balance point, the values of the unknown resistance, inductance, or capacitance can be accurately determined.
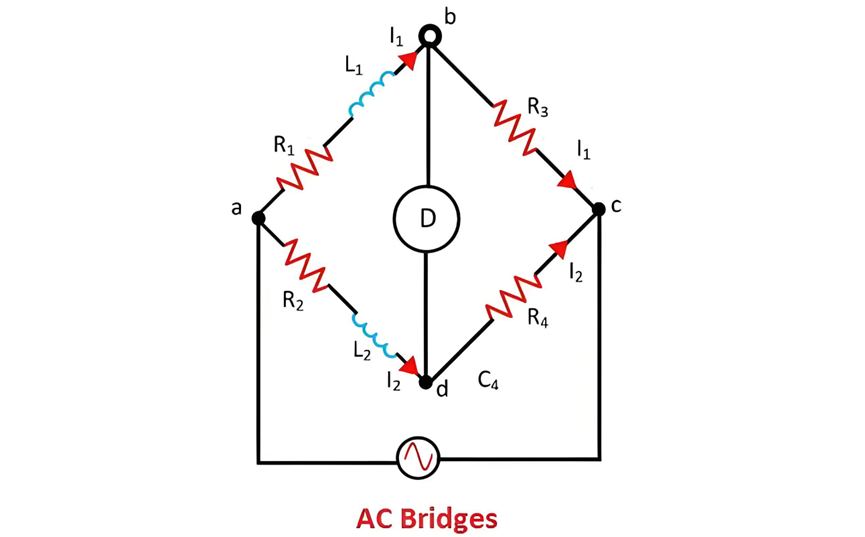
General Equation for an AC Bridge
An AC bridge typically consists of four arms. In many common configurations, two of these arms are composed of non - inductive resistances, while the remaining two arms feature inductances with negligible resistance.
When the AC bridge attains a balanced state,
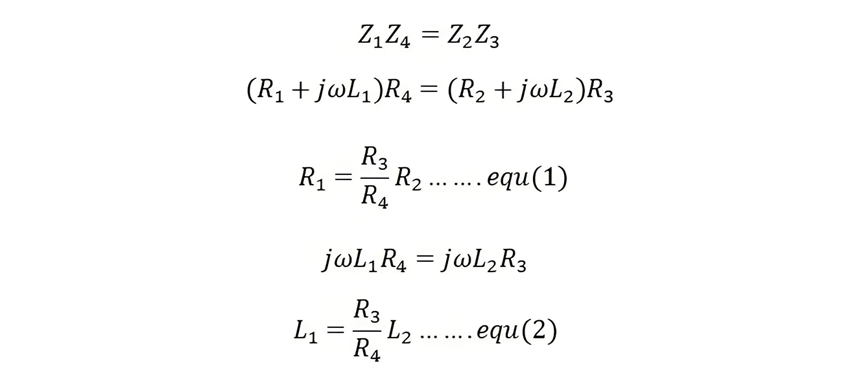
Analysis of AC Bridge Balance Equations
Let l1 and R1 represent the unknown parameters to be measured. These can be determined based on known values R2, R3, R4, and L2. Through an examination of equations (1) and (2), several key insights can be drawn:
- Dual Balance Equations: AC bridges inherently yield two balance equations as a result of their circuit configuration. These equations are fundamental to the operation and analysis of the bridge, providing the necessary mathematical relationships for measurement.
- Parameter Determination: The unknown electrical quantities, which commonly include inductance, capacitance, and resistance, are calculated using these balanced equations. By substituting known values into the equations, engineers can accurately solve for the unknowns, enabling precise measurement of electrical components.
- Frequency - Independence: A notable feature of the balance equations derived from AC bridges is their independence from the frequency of the applied alternating current. This characteristic ensures consistent and reliable measurements across a wide range of frequencies, making AC bridges versatile tools in electrical engineering.
- Diverse Applications: Beyond their primary use in component measurement, AC bridges find extensive application in various other fields. They play a crucial role in communication systems, aiding in signal processing and impedance matching. Additionally, they are integral to complex electronic circuits, where their ability to measure and analyze electrical parameters contributes to the design, optimization, and troubleshooting of these systems.