Transformer On Load Condition - Experts Electrical

Transformer Operation Under Load Conditions

When a transformer is under load, its secondary winding connects to a load, which can be resistive, inductive, or capacitive. A current

I 2

flows through the secondary winding, with its magnitude determined by the terminal voltage

V 2

and load impedance. The phase angle between the secondary current and voltage depends on the load characteristics.

Explanation of Transformer Load Operation

The operational behavior of a transformer under load is detailed as follows:

When the transformer secondary is open-circuited, it draws a no-load current from the main supply. This no-load current induces a magnetomotive force

N 0 I 0

, which establishes a flux Φ in the transformer core. The circuit configuration of the transformer under no-load conditions is illustrated in the diagram below:

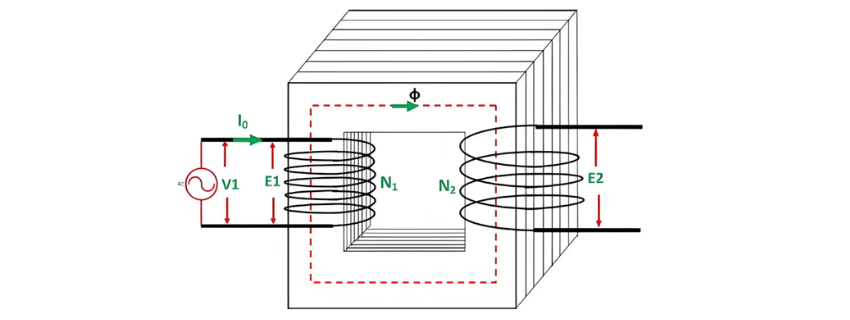
Transformer Load Current Interaction

When a load connects to the transformer secondary, current

I 2

flows through the secondary winding, inducing a magnetomotive force (MMF)

N 2 I 2

. This MMF generates flux ϕ2 in the core, which opposes the original flux ϕ per Lenz's law.

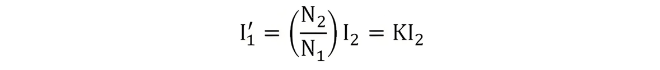
Phase Difference and Power Factor in Transformer

The phase difference between

V1

and

I1

defines the power factor angle ϕ1 on the transformer's primary side. The secondary-side power factor depends on the load type connected to the transformer:

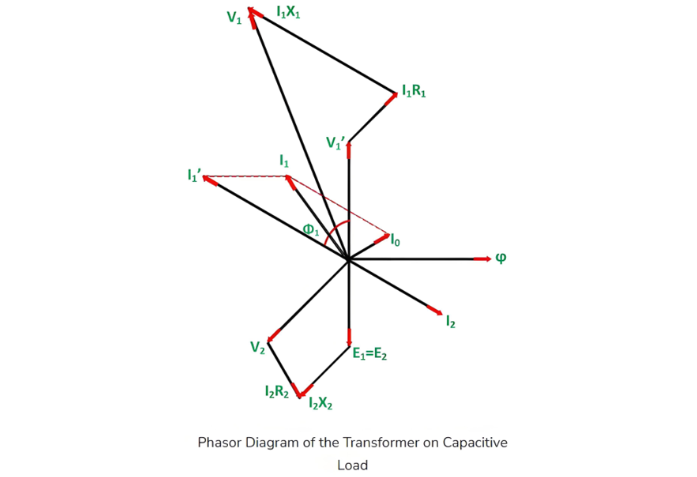
For an inductive load (as shown in the phasor diagram above), the power factor is lagging.
For a capacitive load, the power factor is leading.

The total primary current

I1

is the vector sum of the no-load current

I0

and the counter-balancing current

I'1

, i.e.,

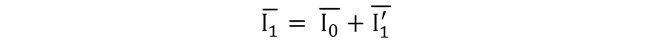
Phasor Diagram of Transformer with Inductive Load

The phasor diagram of an actual transformer under inductive loading is illustrated below:

Steps to Construct the Phasor Diagram

Take flux Φ as the reference.
Induced emfs $E 1$ and $E 2$ lag the flux by 90°.
The primary applied voltage component balancing $E 1$ is denoted as $V' 1$ (i.e., $V'1 = -E1)$ .
No-load current $I0$ lags $V' 1$ by 90°.
For a lagging power factor load, current $I 2$ lags $E 2$ by angle ϕ₂.
Winding resistance and leakage reactance cause voltage drops, making the secondary terminal voltage: $V 2 = E 2 - (voltage drops)$
- $I 2 R$ ₂ is in phase with $I 2$ .
- $I 2 X 2$ is orthogonal to $I 2$ .

Primary current $I 1$ is the phasor sum of $I' 1$ and $I0$ , where $I' 1 = -I 2$ .
Primary applied voltage: $V1 = V'1 + (primary voltage drops)$
- $I 1 R 1$ is in phase with $I 1$ .
- $I 1 X 1$ is orthogonal to $I 1$ .
The phase difference between $V 1$ and $I 1$ defines the primary power factor angle ϕ1.
Secondary power factor:
- Lagging for inductive loads (as in the phasor diagram).
- Leading for capacitive loads.

Steps to Draw Phasor Diagram for Capacitive Load

Take flux Φ as the reference.
Induced emfs $E 1$ and $E 2$ lag the flux by 90°.
The primary applied voltage component balancing $E 1$ is denoted as $V' 1$ (i.e., $V' 1 = -E 1$ ).
No-load current $I 0$ lags $V' 1$ by 90°.
For a leading power factor load, current $I 2$ leads $E 2$ by angle ϕ_$2$.
Winding resistance and leakage reactance cause voltage drops, making the secondary terminal voltage: $V 2 = E 2 - (voltage drops)$
- $I 2 R 2$ is in phase with $I 2$ .
- $I 2 X 2$ is orthogonal to $I 2$ .
Counter-balancing current $I' 1 = -I 2$ (equal in magnitude, opposite in phase to $I 2$ ).
Primary current $I 1$ is the phasor sum of $I' 1$ and $I 0$ : $I^{1} = I^{1'} + I^{0}$
Primary applied voltage $V 1$ is the phasor sum of $V' 1$ and primary voltage drops: $V 1 = V' 1 +(primary voltage drops)$
- $I 1 R 1$ is in phase with $I 1$ .
- $I 1 X 1$ is orthogonal to $I 1$ .
Power factor angles:
- The phase difference between $V 1$ and $I 1$ defines the primary power factor angle ϕ_$1$.
- The secondary power factor (leading for capacitive loads) depends entirely on the connected load type.