Will the voltages of two different currents drawn from an AC source add up?

Will the voltages of two different currents drawn from an AC source add up?

The voltages of two different currents drawn from an AC (Alternating Current) source do not simply add up in the way that might be expected with direct current (DC) sources. To understand why, it's important to consider how voltage and current behave in AC circuits.

Key Concepts in AC Circuits

Impedance (Z): In AC circuits, impedance is the measure of the total opposition that a circuit presents to a current due to the presence of resistance (R), inductance (L), and capacitance (C). Impedance is a complex quantity that includes both magnitude and phase angle.

Phase Relationship: In AC circuits, the voltage and current can be out of phase due to the presence of reactive components like inductors and capacitors. This phase difference is critical when considering the behavior of voltage and current.

Vector Addition: Unlike DC circuits, where voltage drops across components can be added algebraically, in AC circuits, voltage drops must be added vectorially because they can be out of phase.

Voltage and Current Relationships

In an AC circuit, the relationship between voltage (V), current (I), and impedance (Z) is given by:

V=I⋅Z

Here, V, I, and Z are all phasors, which include both magnitude and phase information.

Two Different Currents Drawn from an AC Source

Consider a scenario where two different currents (I1and I2) are drawn from an AC source. Each current will have its own impedance (Z1 and Z2) and associated voltage (V1 and V2)：

V1=I1⋅Z

V2=I2⋅Z

If these currents are flowing through different parts of the same circuit or different branches in parallel, the voltages across each branch (V1and V2) do not simply add up. Instead, the total voltage across the entire circuit depends on the configuration of the circuit and the phase relationships between the currents and voltages.

Parallel Connection

If the two currents (I1 and I2) are flowing through different branches in parallel, the voltages across each branch will be the same because they share a common node:

V1=V2=V

In this case, the total current (I total) is the sum of the individual currents:

I total=I1+I2

Series Connection

If the two currents (I1 and I2) are flowing through different components in series, the total voltage across the series combination will be the vector sum of the individual voltages:

V total=V1+V2

However, because V1and V2are phasors, the addition must account for the phase differences:

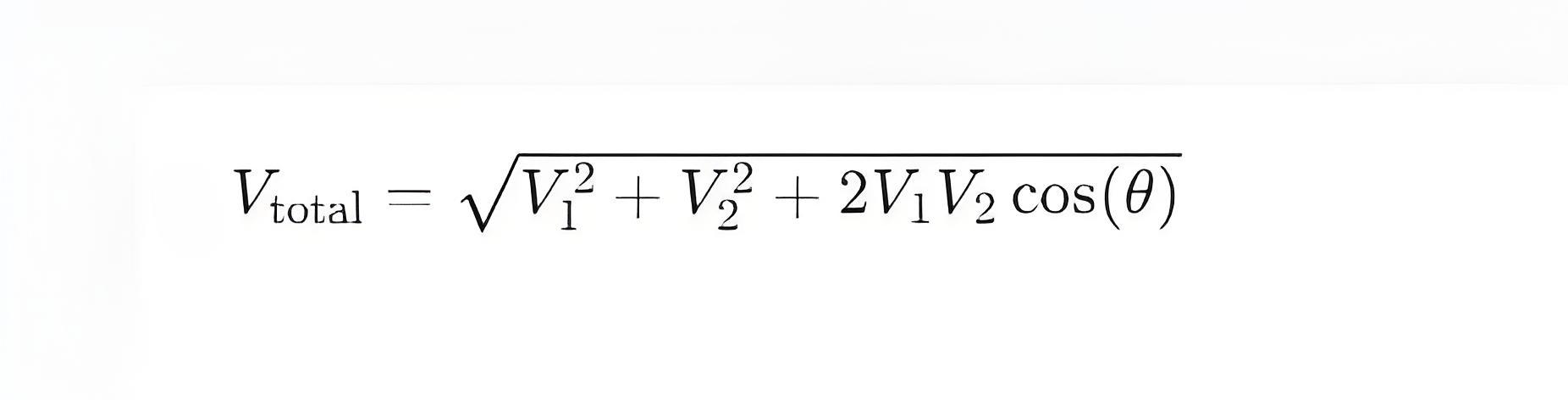
θ is the phase angle between V1and V 2

Summary

In summary, the voltages of two different currents drawn from an AC source do not simply add up because:

• Phase Differences: Voltages in AC circuits must be considered with respect to phase differences.

• Complex Impedances: Impedances involve both magnitude and phase, affecting the relationship between voltage and current.