Maximum Power Transfer Theorem

Maximum Power Transfer Theorem

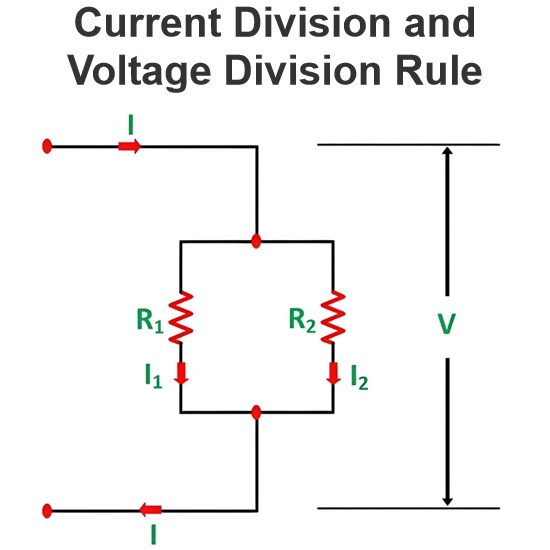
Suppose we have a voltage source or battery that’s internal resistance is Ri and a load resistance RL is connected across this battery. Maximum power transfer theorem determines the value of resistance RL for which, the maximum power will be transferred from source to it. Actually the maximum power, drawn from the source, depends upon the value of the load resistance. There may be some confusion let us clear it.

Power delivered to the load resistance,

To find the maximum power, differentiate the above expression with respect to resistance RL and equate it to zero. Thus,

Thus in this case, the maximum power will be transferred to the load when load resistance is just equal to internal resistance of the battery.

Maximum power transfer theorem can be applicable in complex network as follows-
A resistive load in a resistive network will abstract maximum power when the load resistance is equal to the resistance viewed by the load as it looks back to the network. Actually this is nothing but the resistance presented to the output terminals of the network. This is actually Thevenin equivalent resistance as we explained in Thevenin’s theorem if we consider the whole network as a voltage source. Similarly, if we consider the network as current source, this resistance will be Norton equivalent resistance as we explained in Norton theorem.

Source: Electrical4u.

Statement: Respect the original, good articles worth sharing, if there is infringement please contact delete.