What is a First Order Control System?
What is a First Order Control System?
First Order Control System Definition
A first order control system uses a simple type of differential equation to relate inputs and outputs, focusing on the first derivative of time only.
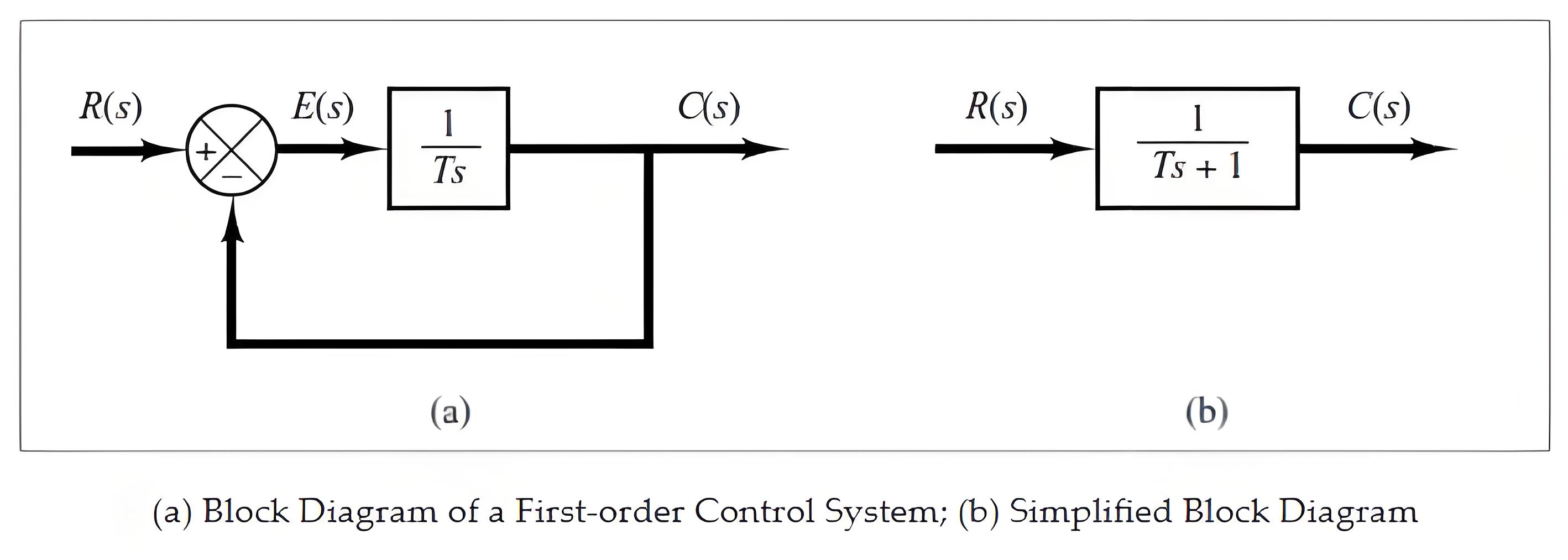
The transfer function (input-output relationship) for this control system is defined as:
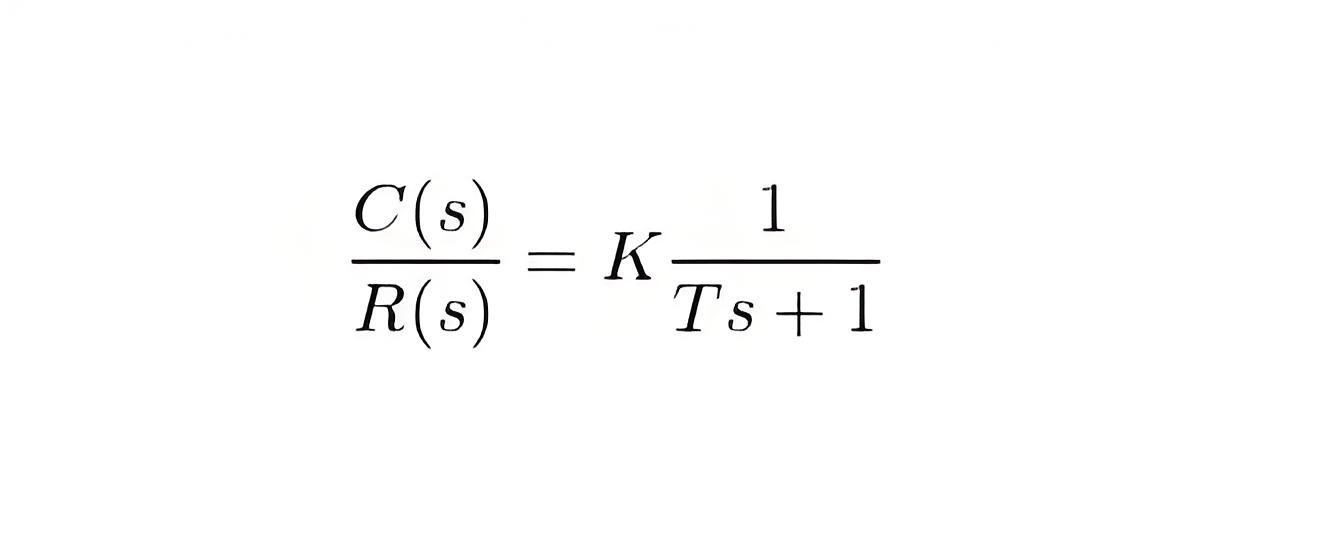
K is the DC Gain (DC gain of the system ratio between the input signal and the steady-state value of output)
T is the time constant of the system (the time constant is a measure of how quickly a first-order system responds to a unit step input).
First Order Control System Transfer Function
A transfer function represents the relationship between the output signal of a control system and the input signal, for all possible input values.
Poles of a Transfer Function
The poles of the transfer function are the value of Laplace Transform variable(s), which cause the transfer function to become infinite.The denominator of a transfer function is actually the poles of function.
Zeros of a Transfer Function
The zeros of the transfer function are the values of the Laplace Transform variable(s), that causes the transfer function becomes zero.The nominator of a transfer function is actually the zeros of the function.
First Order Control System
Here we discuss the first-order control system without zeros. The first-order control system tells us the speed of the response that what duration it reaches the steady-state.If the input is a unit step, R(s) = 1/s so the output is a step response C(s). The general equation of 1st order control system is , i.e is the transfer function.
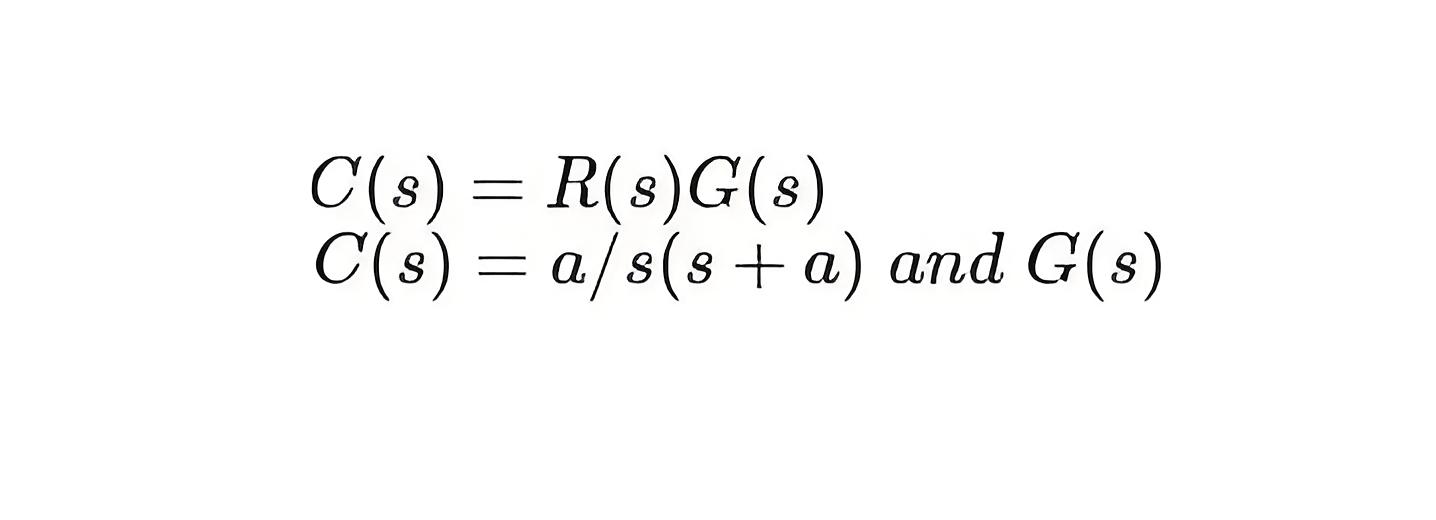
There are two poles, one is the input pole at the origin s = 0 and the other is the system pole at s = -a, this pole is at the negative axis of the pole plot.Using MATLAB’s pzmap command, we can identify the poles and zeros of the system, crucial for analyzing its behavior.We now taking the inverse transform so total response become which is the sum of forced response and natural response.
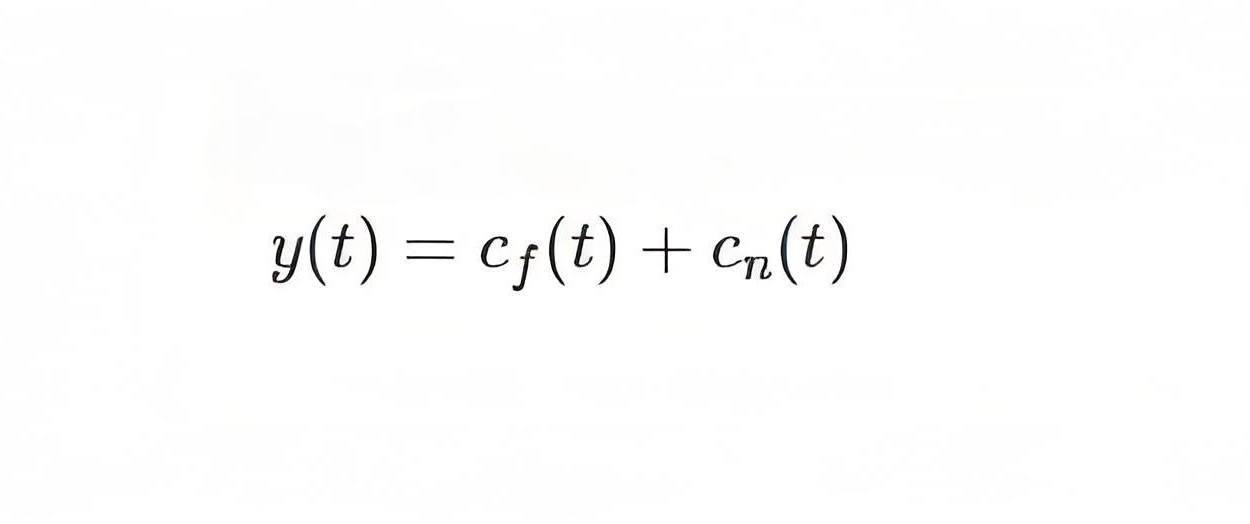
Due to the input pole at the origin, produces the forced response as name describe by itself that giving forced to the system so it produces some response which is forced response and the system pole at -a produces a natural response which is due to the transient response of the system.
After some calculation, here General form of the first-order system is C(s) = 1-e-at that is equal to forced response which is “1” and natural response which is equal to “e-at”. The only thing which is needed to find is the parameter “a”.
Many techniques like a differential equation or inverse Laplace Transform, these all solve the total response but these are time-consuming and laborious.
The use of poles, zeros, and there some fundamental concept gives us the qualitative information to solve the problems and due to these concepts, we can easily tell the speed of response and the time of a system to reach the steady-state point.
Let us describe the three transient response performance specifications, the time constant, rise time, and settling time for a first-order control system.
Time Constant of a First Order Control System
The time constant can be defined as the time it takes for the step response to rise up to 63% or 0.63 of its final value. We refer to this as t = 1/a. If we take reciprocal of time constant, its unit is 1/seconds or frequency.
We call the parameter “a” the exponential frequency. Because the derivative of e-at is -a at t = 0. So the time constant is considered as a transient response specification for a first-order control system.
We can control the speed of response by setting the poles. Because the farther the pole from the imaginary axis, the faster the transient response is. So, we can set poles farther from the imaginary axis to speed up the whole process.
Rise Time of a First Order Control System
The rise time is defined as the time for the waveform to go from 0.1 to 0.9 or 10% to 90% of its final value. For the equation of rising time, we put 0.1 and 0.9 in the general first-order system equation respectively.
For t = 0.1
For t = 0.9
Taking the difference between 0.9 and 0.1
Here the equation of rising time. If we know the parameter of a, we can easily find the rise time of any given system by putting “a” in the equation.
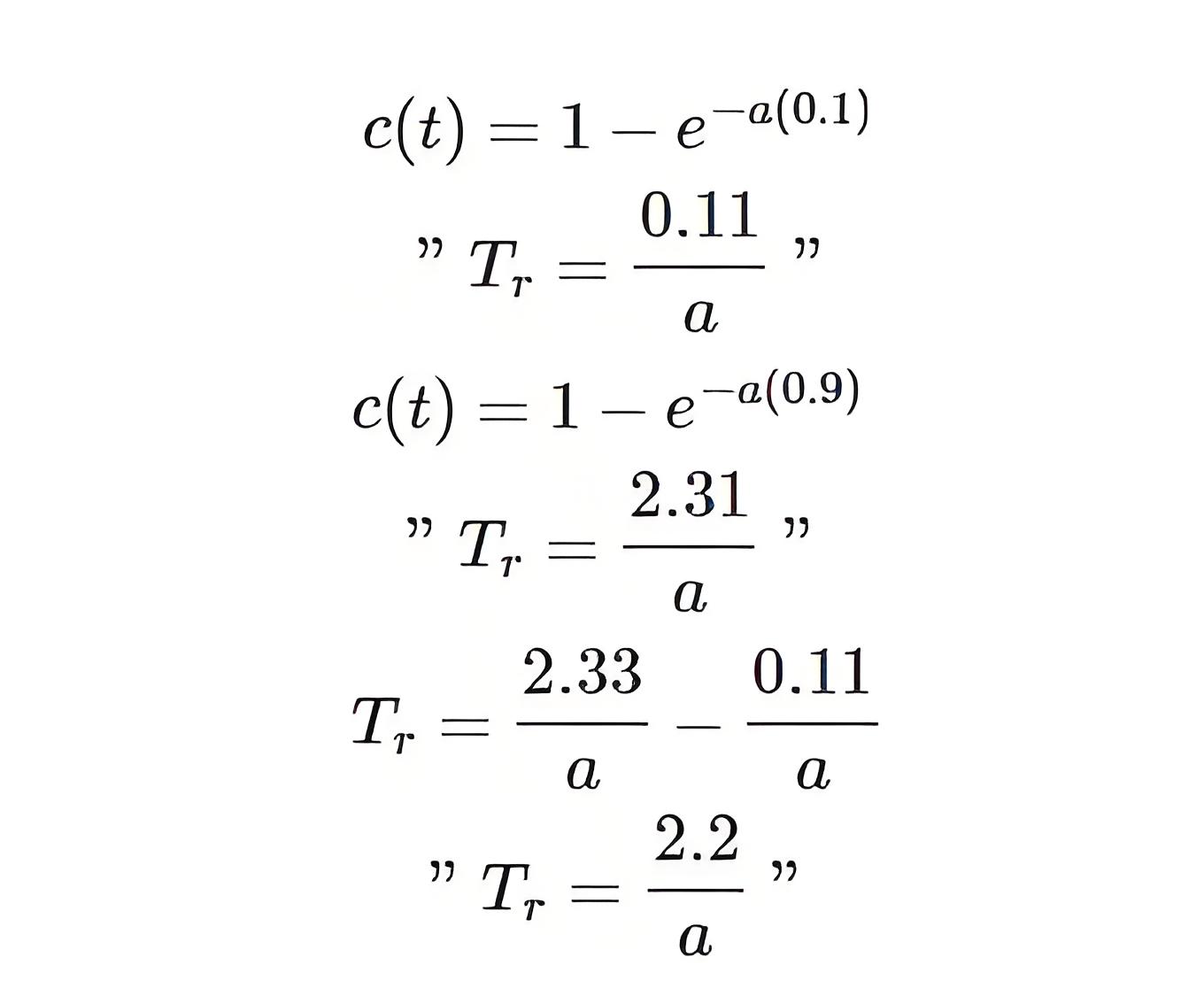
Settling Time of a First Order Control System
The settling time is defined as the time for the response to reach and stay within 2% of its final value. We can limit the percentage up to 5% of its final value. Both percentages are a consideration.
The equation of settling time is given by Ts = 4/a.
By using these three transient response specifications, we can easily compute the step response of a given system that’s why this qualitative technique is useful for order systems equations.
Conclusion of First Order Control Systems
After learning all things related to 1st order control system, we come to the following conclusions:
A pole of the input function generates the form of the forced response. It is because of the pole at the origin which generates a step function at the output.
A pole of the transfer function generates a natural response. It the pole of the system.
A pole on the real axis generates an exponential frequency of the form e-at. Thus, the farther the pole to the origin, the faster the exponential transient response will decay to zero.
Understanding poles and zeros allows us to enhance system performance and achieve faster, more accurate outputs.
The Electricity Encyclopedia is dedicated to accelerating the dissemination and application of electricity knowledge and adding impetus to the development and innovation of the electricity industry.