Control Systems Block Diagram
Block Diagram Definition
A block diagram is used to represent a control system in diagram form. In other words, the practical representation of a control system is its block diagram. Each element of the control system is represented with a block and the block is the symbolic representation of the transfer function of that element.
It is not always convenient to derive a complex control system’s entire transfer function in a single function. It is easier to derive the transfer function of the control element connected to the system separately.
Each block represents an element’s transfer function and is connected along the signal flow path.Block diagrams simplify complex control systems. Each control system element is shown as a block, symbolizing its transfer function. Together, these blocks form the complete control system.
The figure below shows two elements with transfer function Gone(s) and Gtwo(s). Where Gone(s) is the transfer function of the first element and Gtwo(s) is the transfer function of the second element of the system.
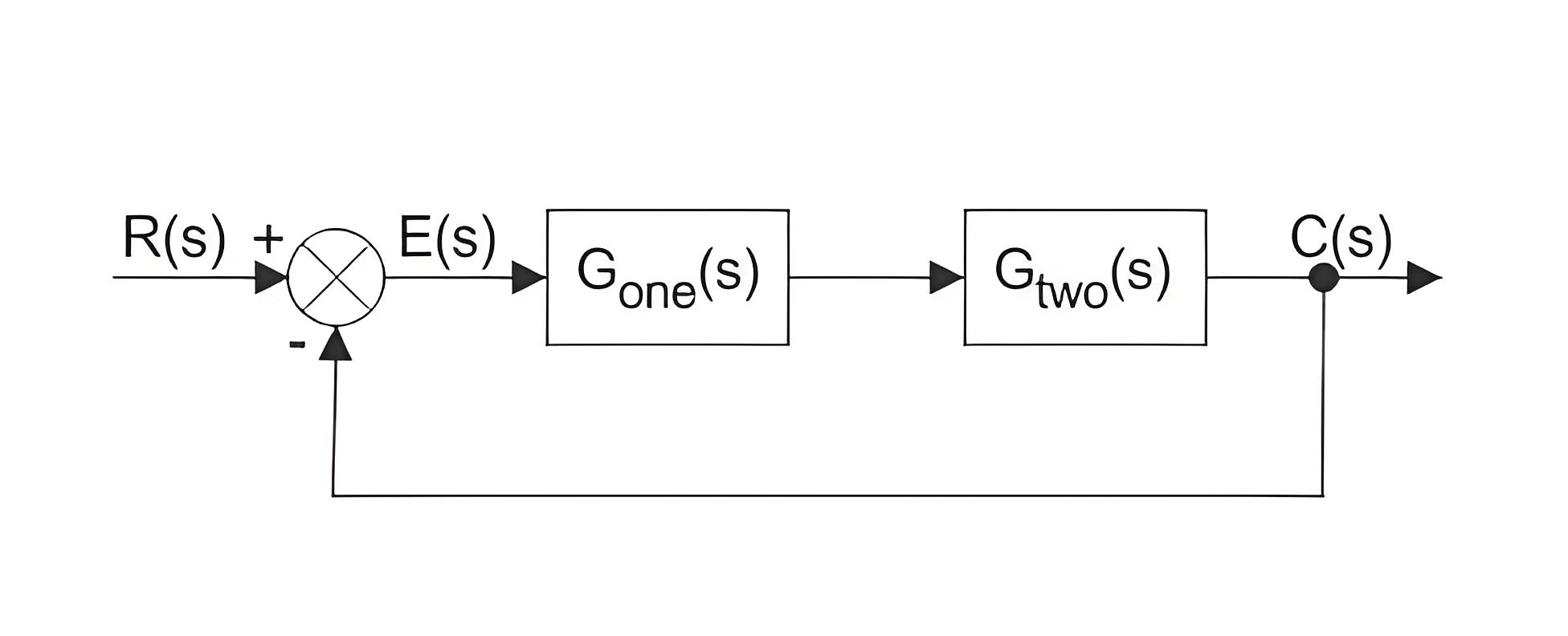
The diagram also shows there is a feedback path through which output signal C(s) is fed back and compared with the input R(s). The difference between input and output is which is acting as the actuating signal or error signal.
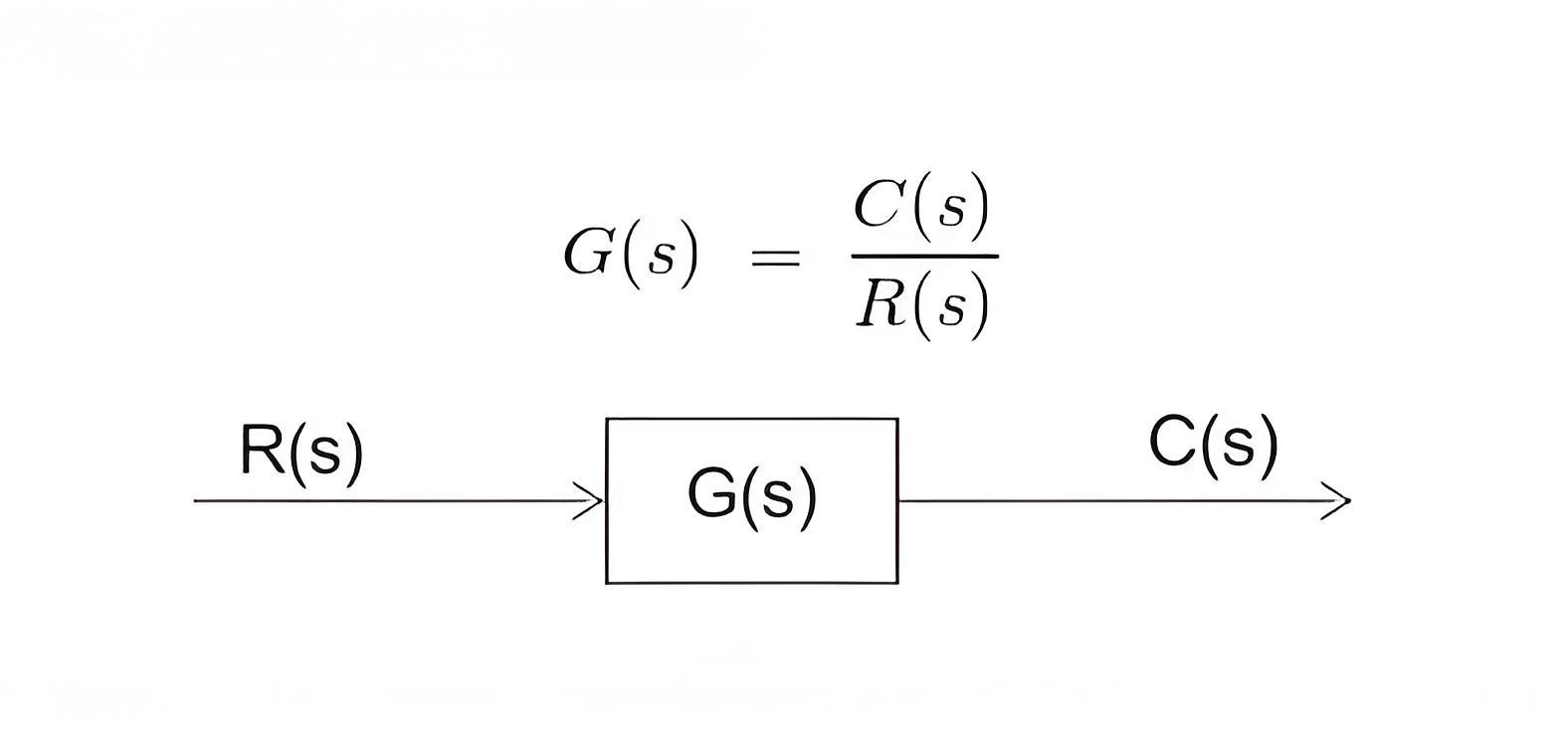
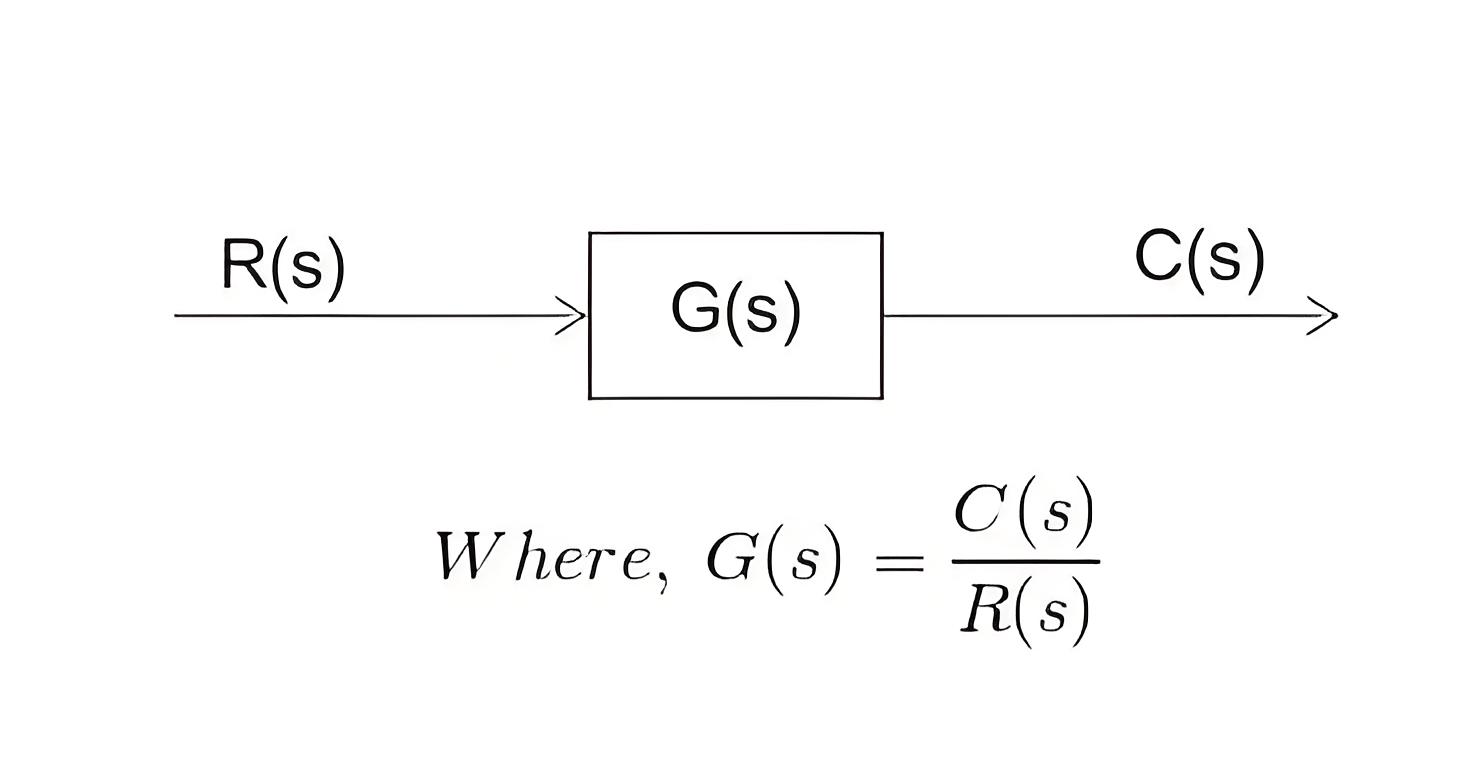
In each block of the diagram, the output and input are related together by a transfer function. Where the transfer function is:
Where C(s) is the output and R(s) is the input of that particular block.A complex control system consists of several blocks. Each of them has its own transfer function. But the overall transfer function of the system is the ratio of the transfer function of the final output to the transfer function of the system’s initial input.
This system’s overall transfer function can be obtained by simplifying the control system by combining these individual blocks, one by one.The technique of combining these blocks is referred to as the block diagram reduction technique.For the successful implementation of this technique, some rules for block diagram reduction to be followed.
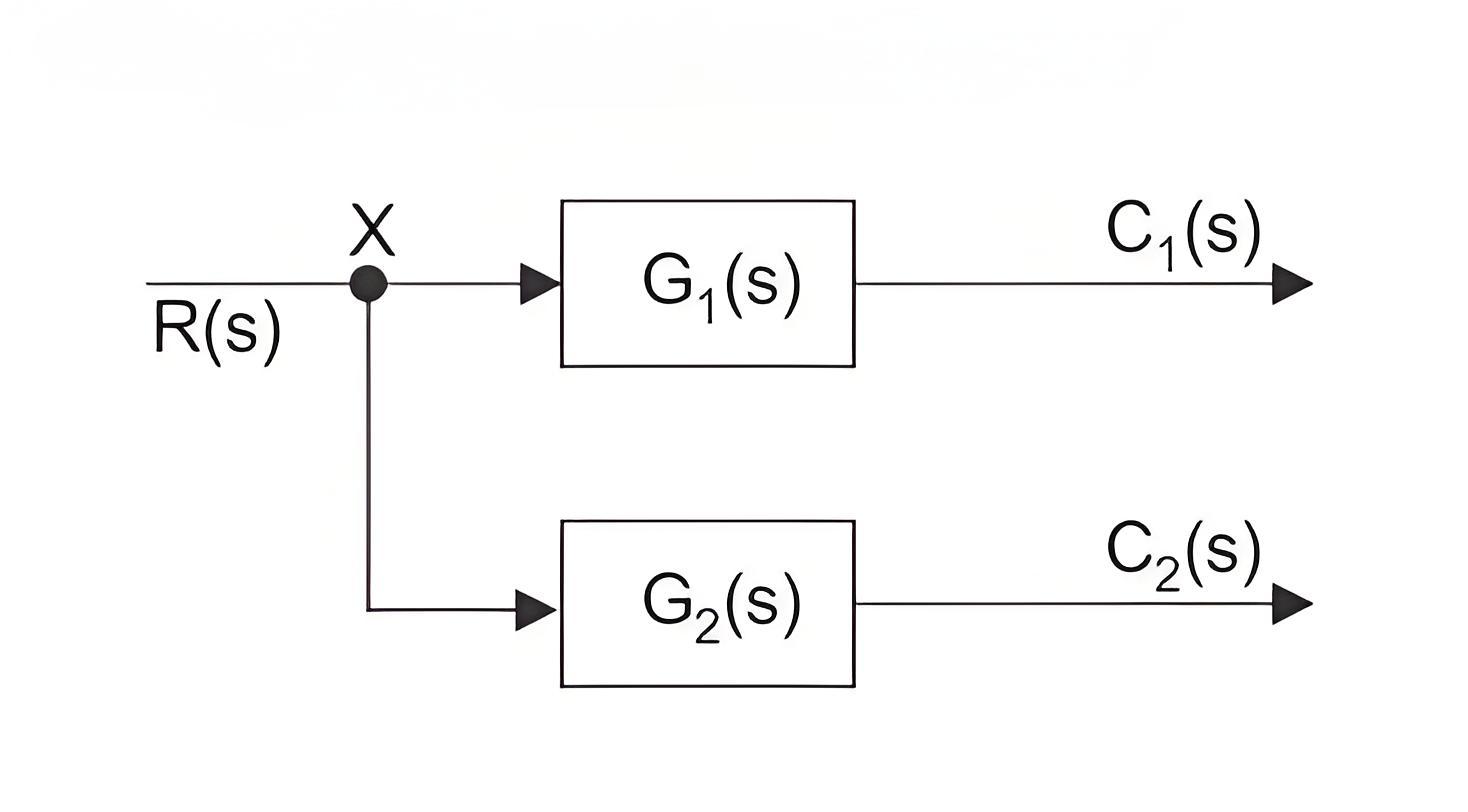
Take off Point in a Control System Block Diagram
When we need to apply one or the same input to more than one block, we use what’s known as the take-off point.This point is where the input has more than one path to propagate. Note that the input does not get divided at a point.
But instead, the input propagates through all the paths connected to that point without affecting its value.Hence, the same input signals can be applied to more than one system or block by having a take-off point.A common input signal representing more than one block of a control system is done by a common point, as shown in the figure below with point X.
Cascade Blocks
When control blocks are connected in series (cascaded), the overall transfer function is the product of all individual block transfer functions.Also, remember that a block’s output is not influenced by other blocks in the series.
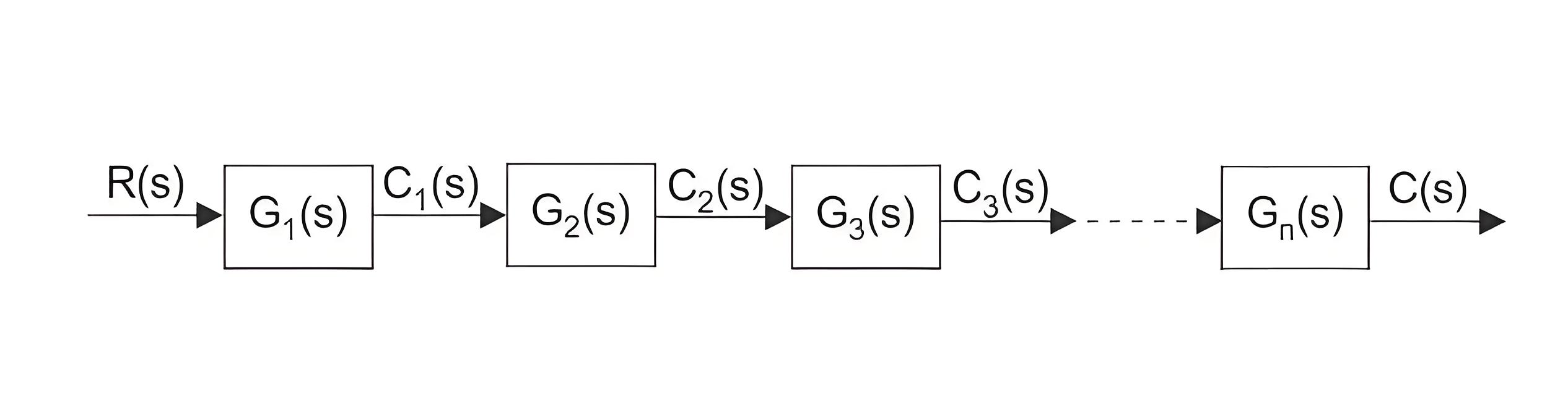
Now, from the diagram, it is seen that,
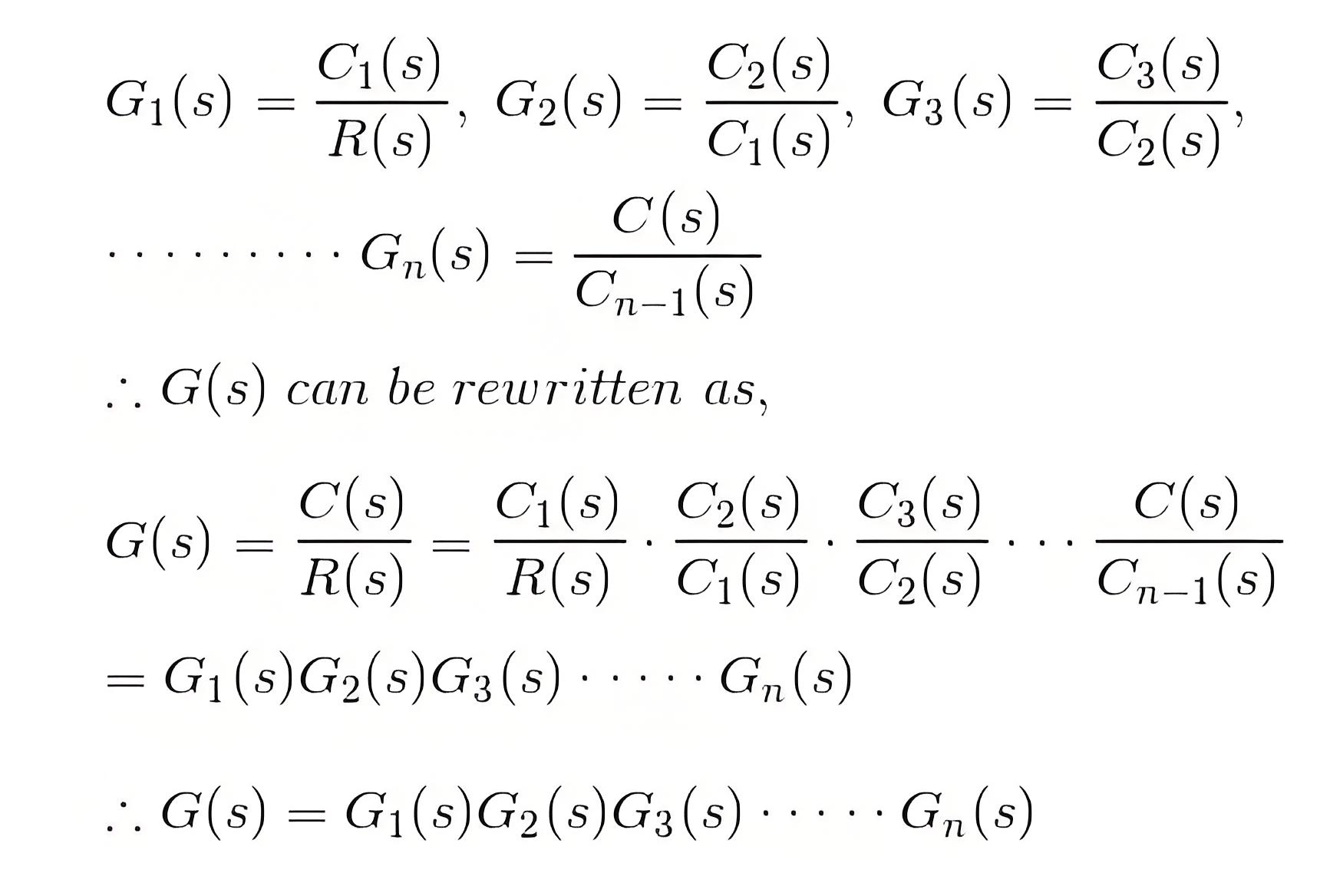
Where G(s) is the overall transfer function of the cascaded control system.

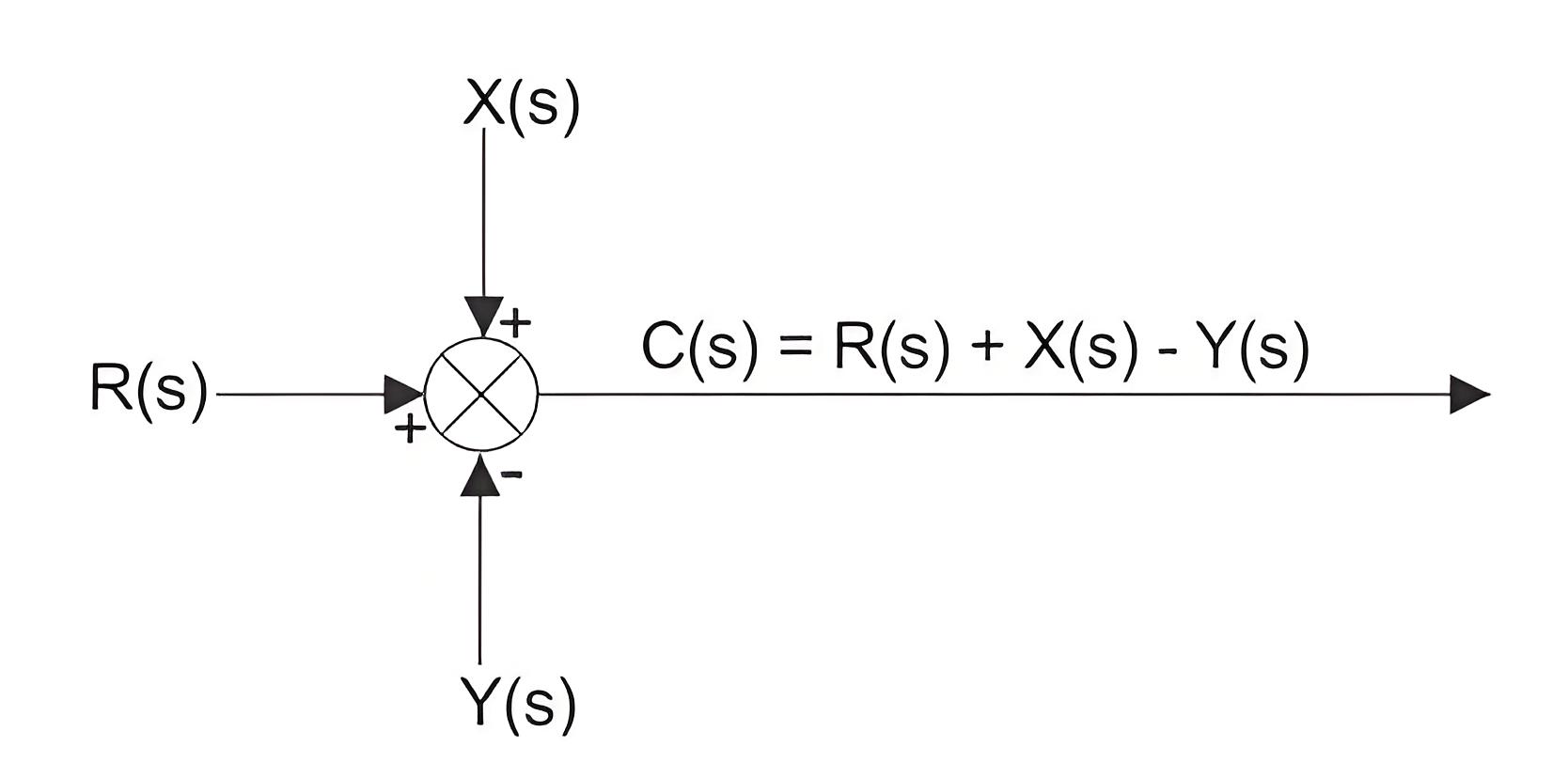
Summing Points in a Control System Block Diagram
Sometimes, different input signals are applied to the same block instead of a single input to multiple blocks.Here, the combined input signal is the sum of all applied input signals. This summation point, where inputs merge, is shown as a crossed circle in diagrams.
Here R(s), X(s), and Y(s) are the input signals. It is necessary to indicate the fine specifying the input signal entering a summing point in the control system’s block diagram.
Consecutive Summing Points
A summing point with more than two inputs can be divided into two or more consecutive summing points, where alteration of the position of consecutive summing points does not affect the signal’s output.
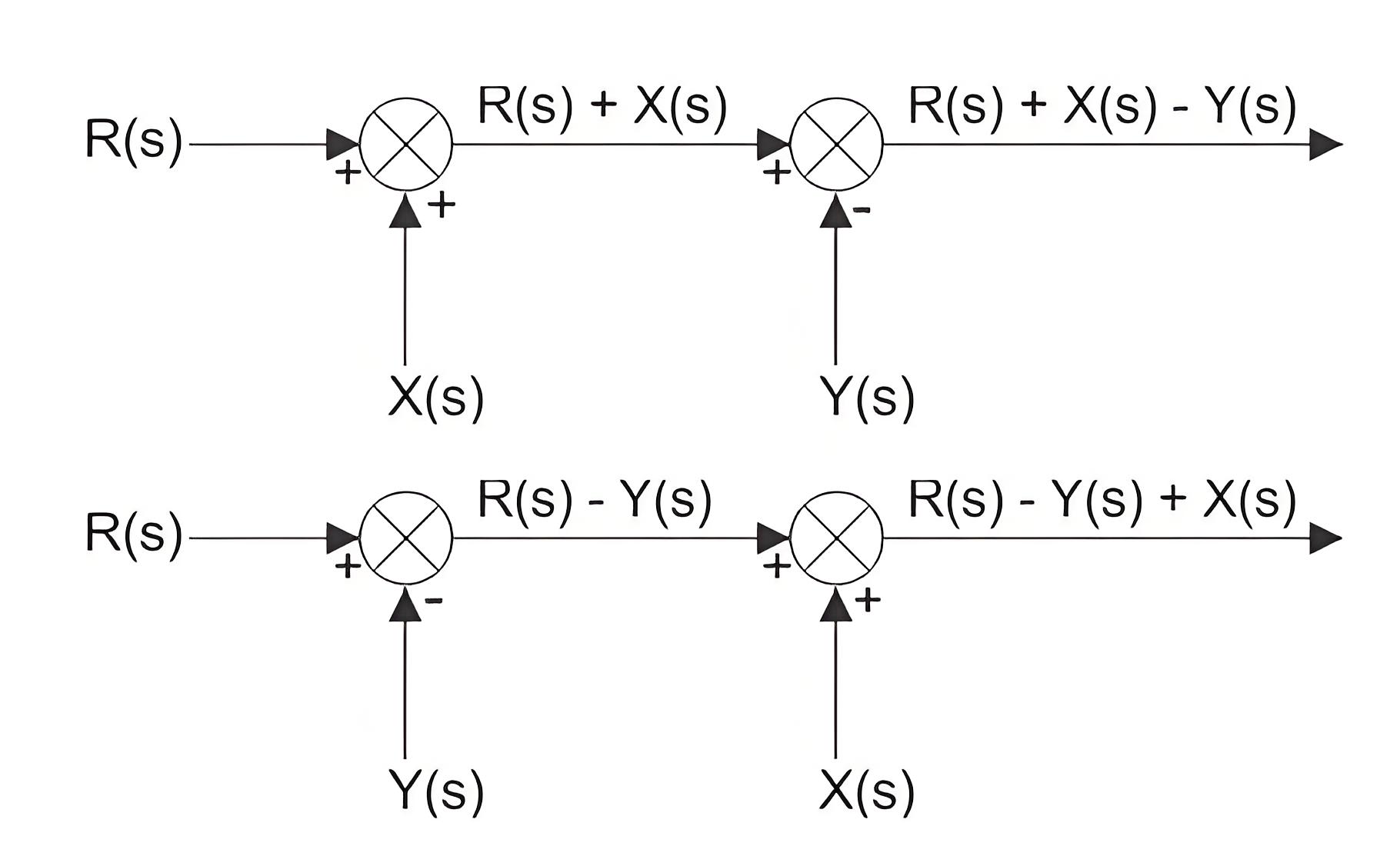
In other words – if there is more than one summing point directly inter associated, and then they can be easily interchanged from their position without affecting the final output of the summing system.
Parallel Blocks
When the same input signal is applied, different blocks and the output from each of them are added in a summing point for taking the system’s final output.
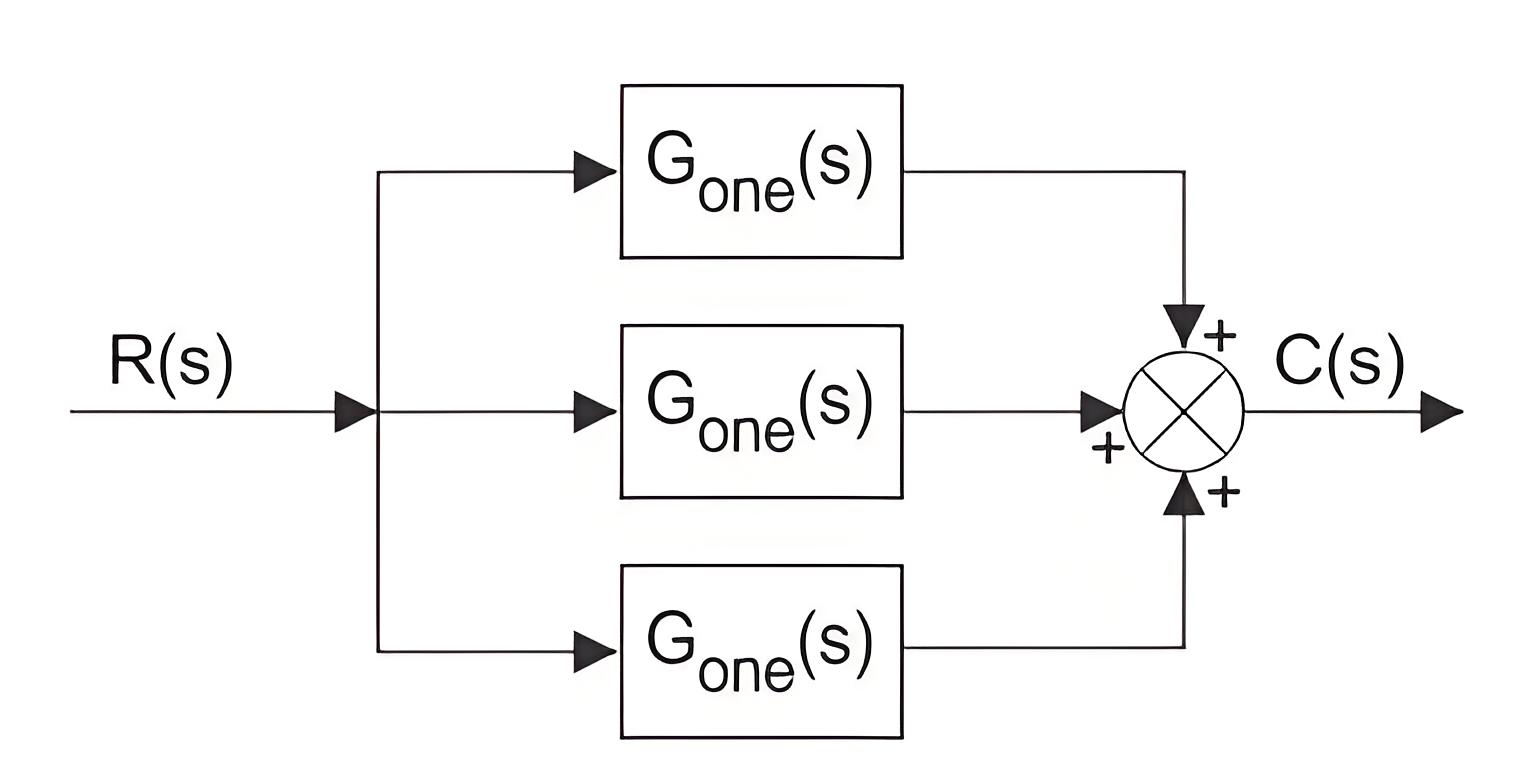
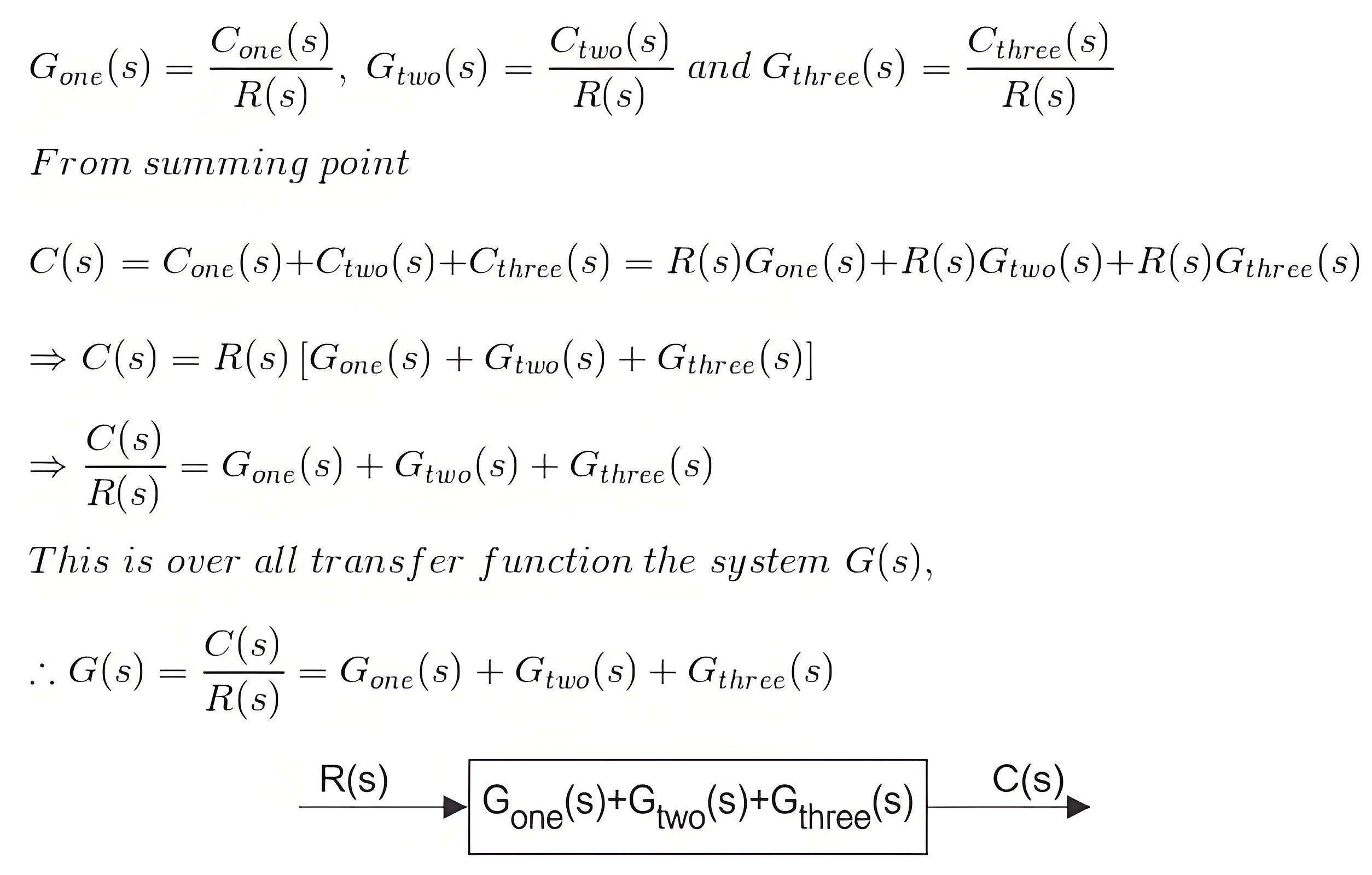
The system’s overall transfer function will be the algebraic sum of the transfer function of all individual blocks.
If Cone, Ctwo, and Cthree are the blocks’ outputs with transfer function Gone, Gtwo, and Gthree, then.
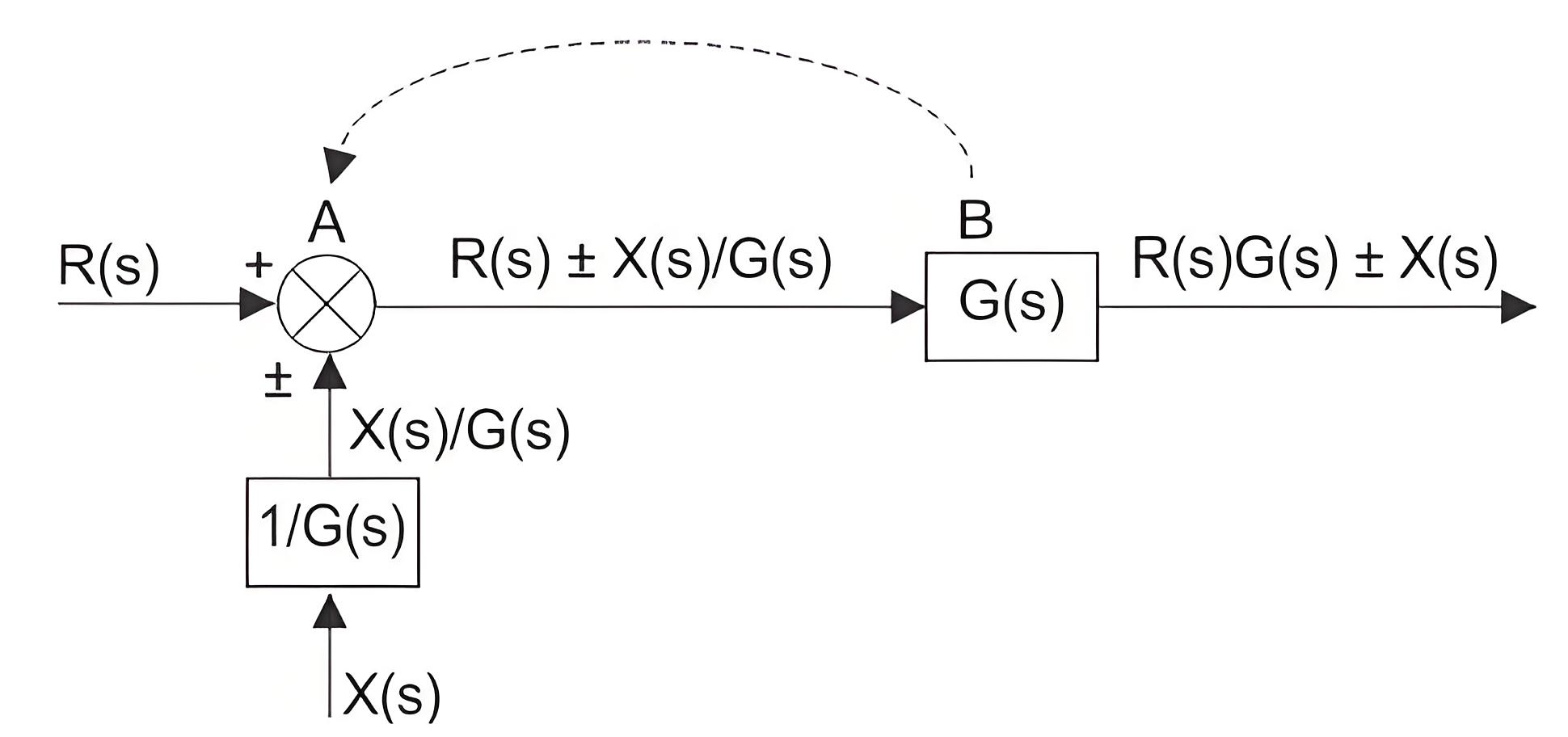
Shifting of Takeoff Point
If the same signal is applied to more than one system, then the signal is represented in the system by a point called the take-off point.The principle of shifting the take-off point is that it may be shifted on either side of a block, but the branches’ final output connected to the take-off point must be un-changed.
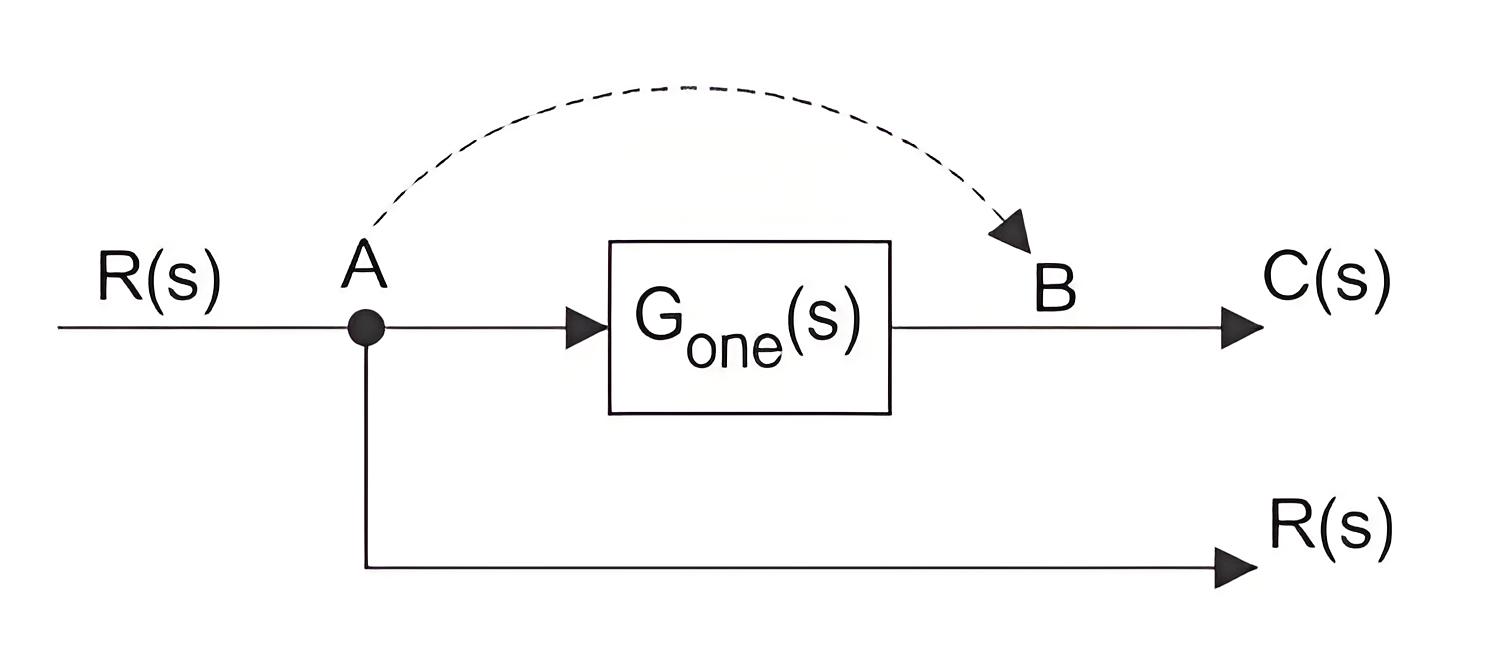
The take-off point can be shifted to either side of the block.
In the figure above, the take-off point is shifted from position A to B. The signal R(s) at take-off point A will become G(s)R(s) at point B.
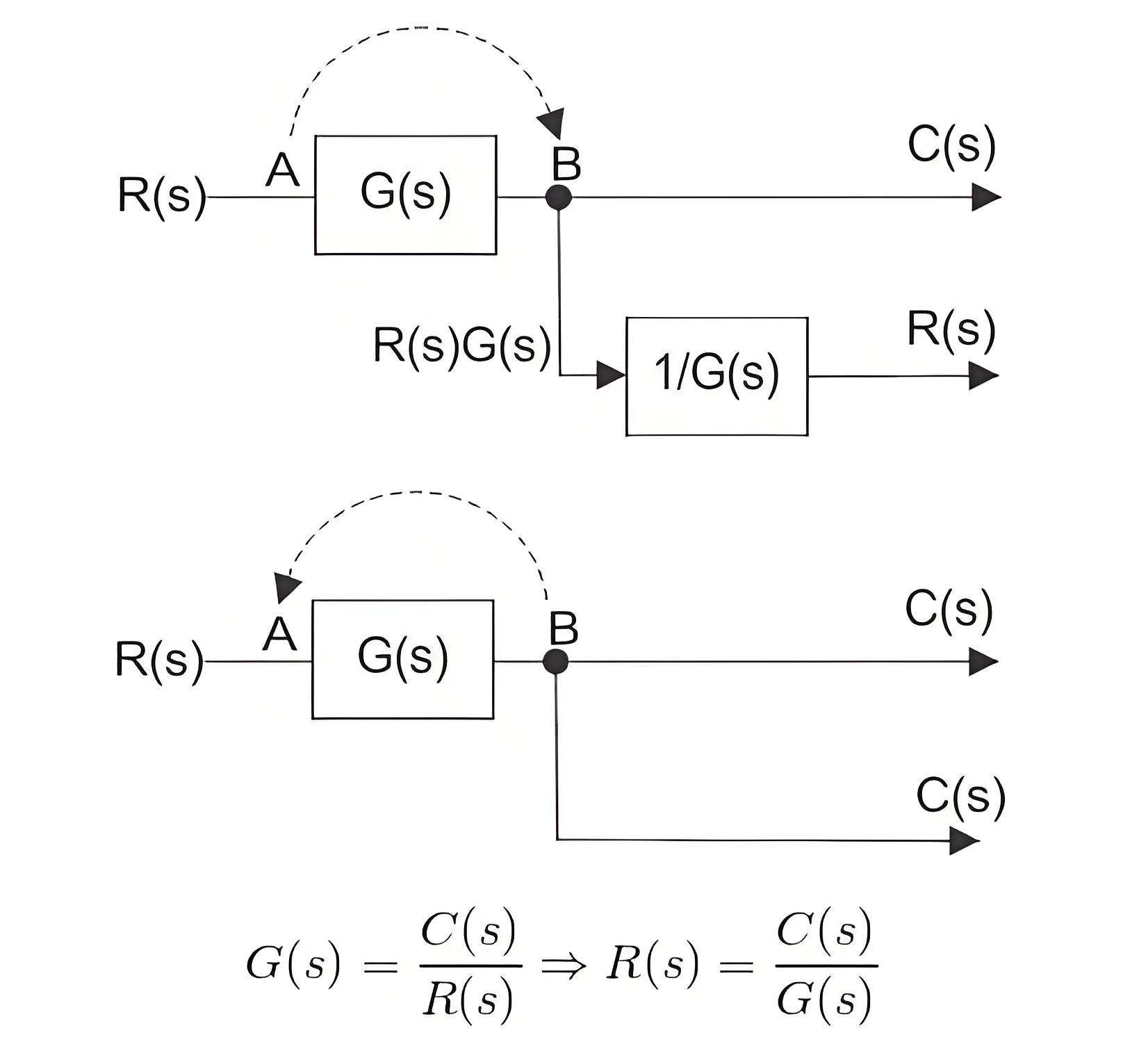
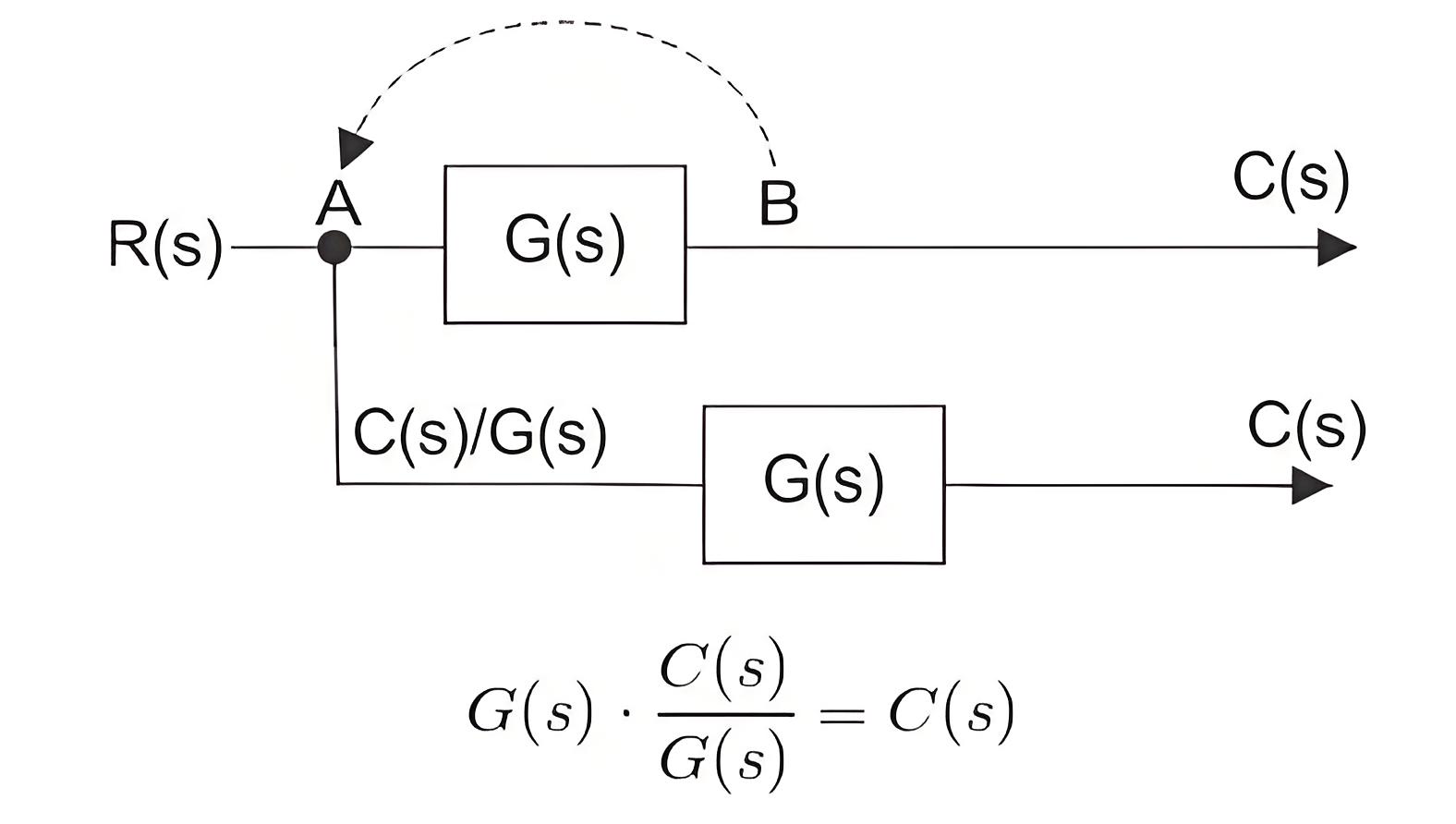
Hence another block of the inverse of transfer function G(s) is to be put on that path to get R(s) again.Now let us examine when the take-off point is shifted before the block, which was previously after the block.Here the output is C(s), and the input is R(s) and hence.
Here, we have to put one block of transfer function G(s) on the path so that output again comes as C(s).
Shifting of Summing Point
Let us examine the summing point shifting from a position before a block to a position after a block.There are two input signals, R(s) and ± X(s), entering in a summing point at position A. The output of the summing point is R(s) ± X(s).The resultant signal is the input of a control system block of transfer function G(s), and the final output of the system is
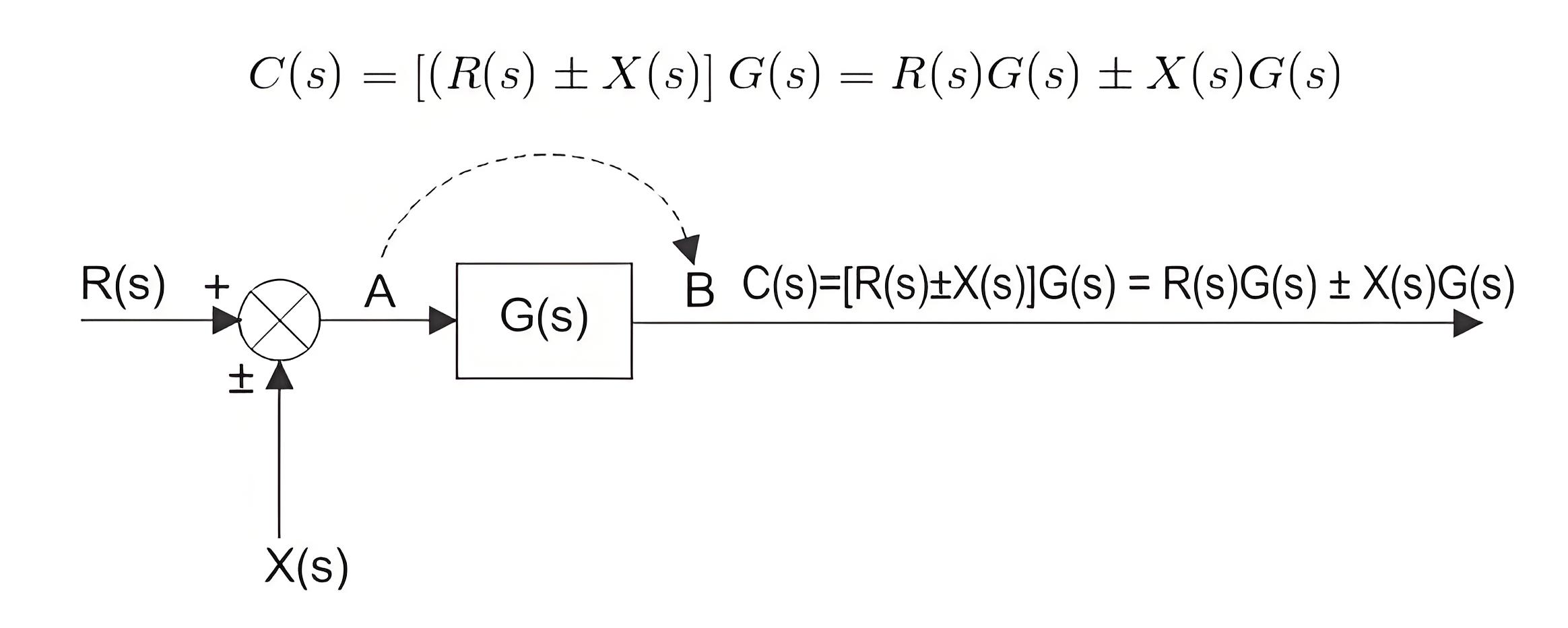
Hence, a summing point can be redrawn with input signals R(s)G(s) and ± X(s)G(s)
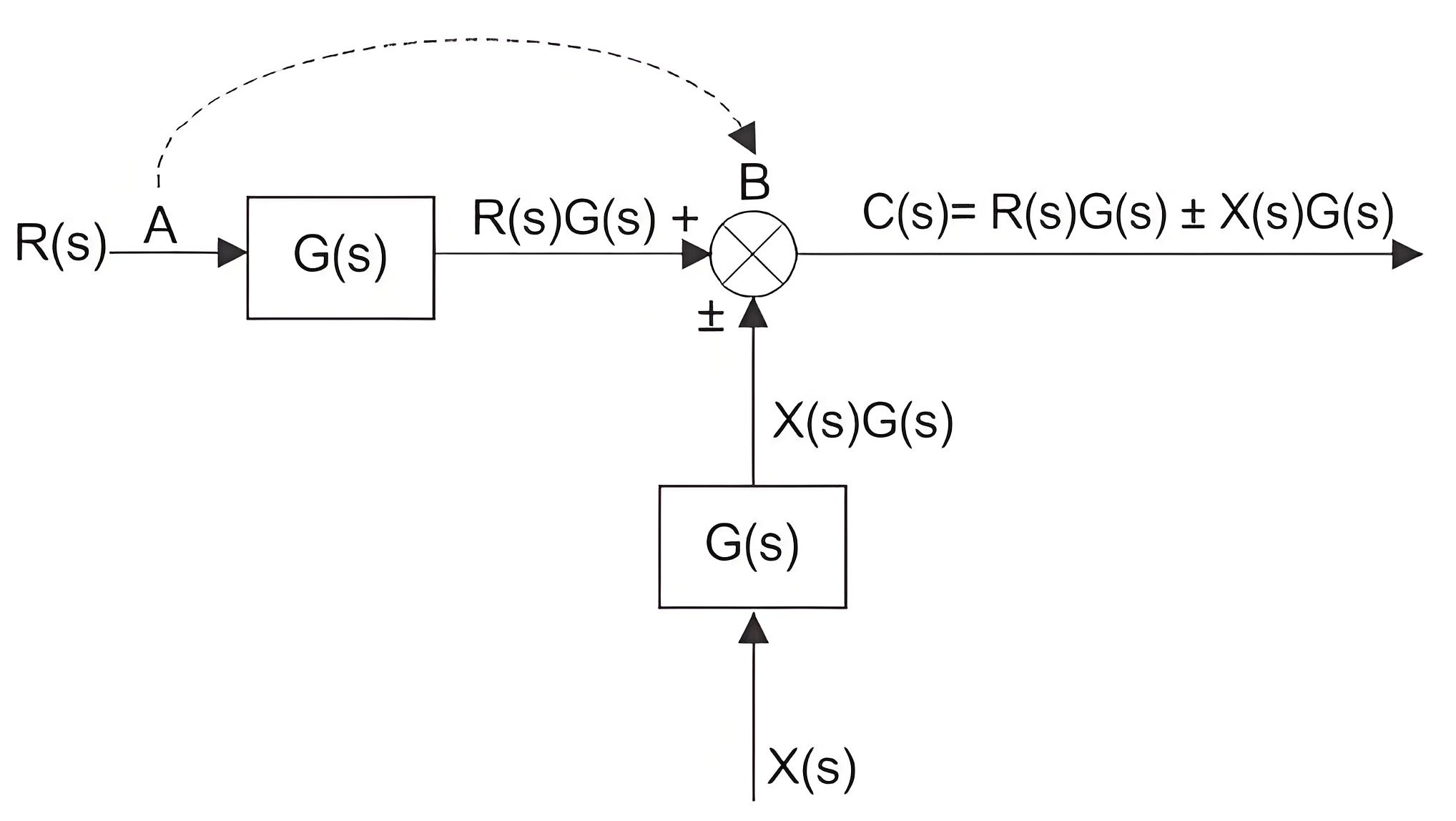
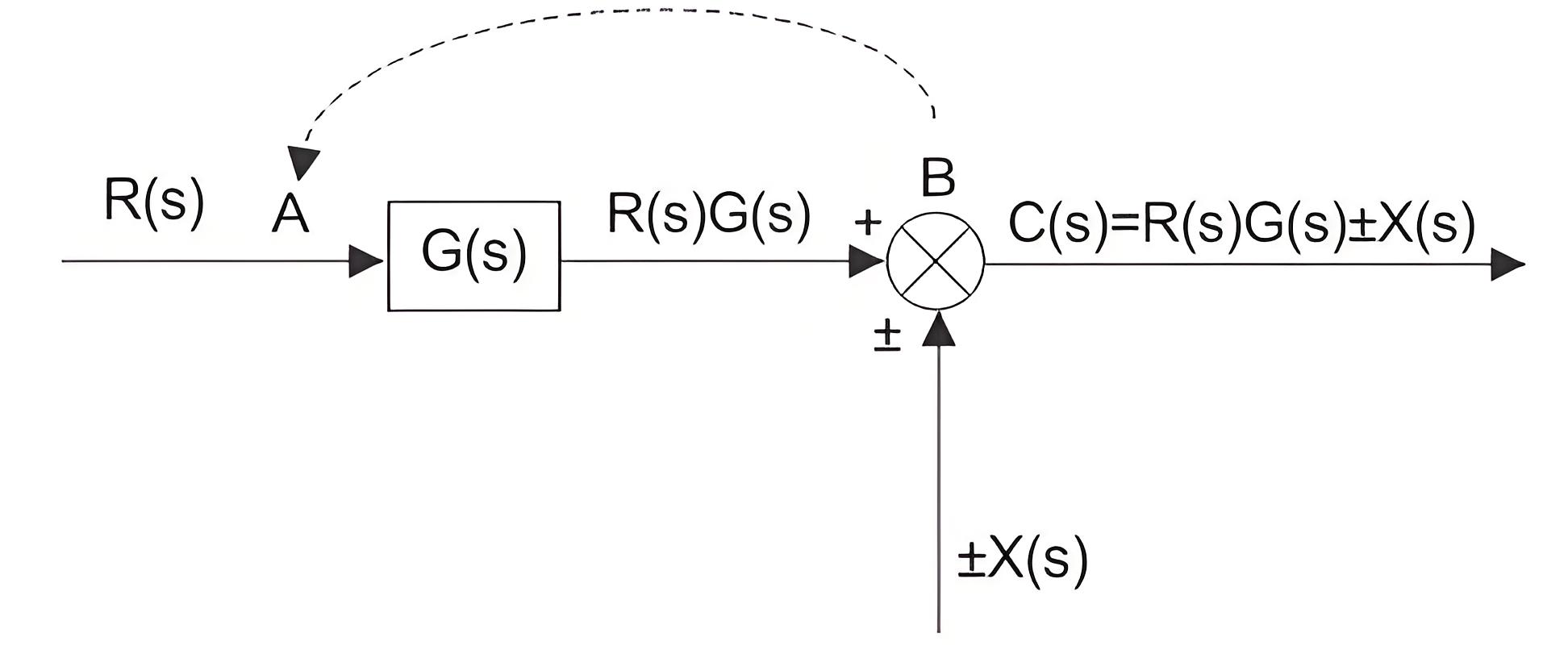
The above block diagrams of control system output can be rewritten as
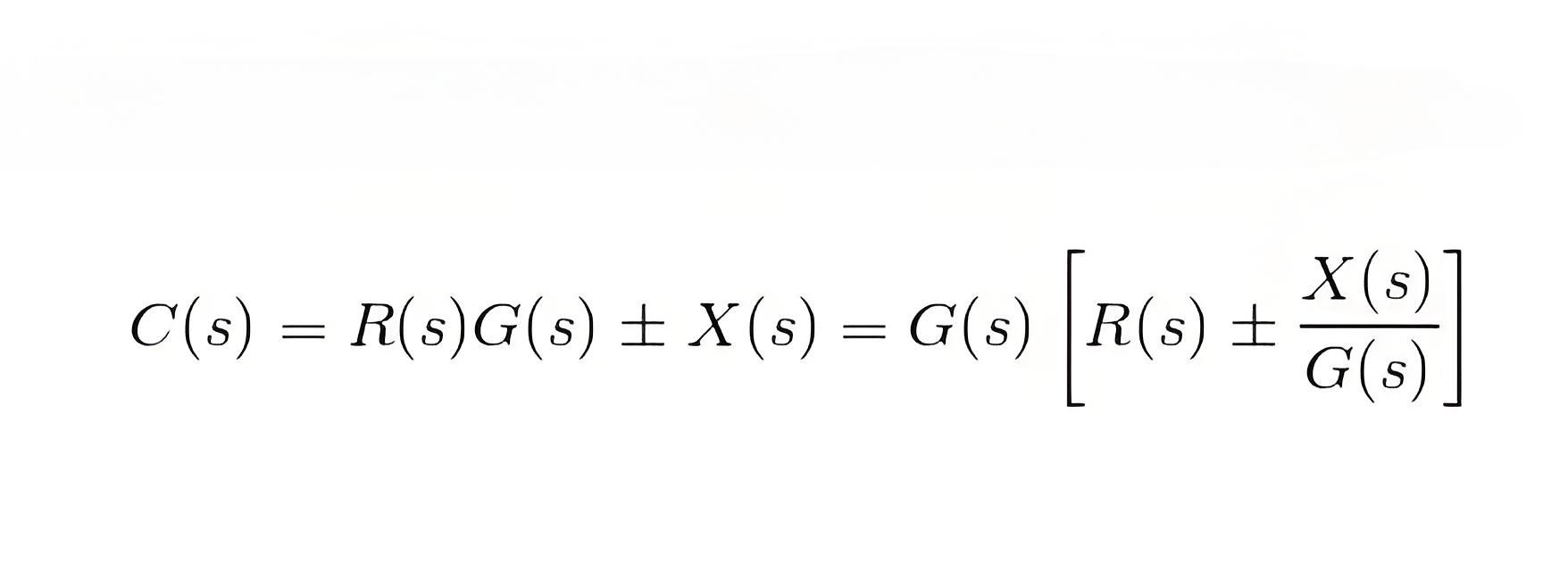
The above equation can be represented by a block of transfer function G(s) and input R(s) ± X(s)/G(s) again R(s)±X(s)/G(s) can be represented with a summing point of input signal R(s) and ± X(s)/G(s) and finally it can be drawn as below.
Block Diagram of Closed Loop Control System
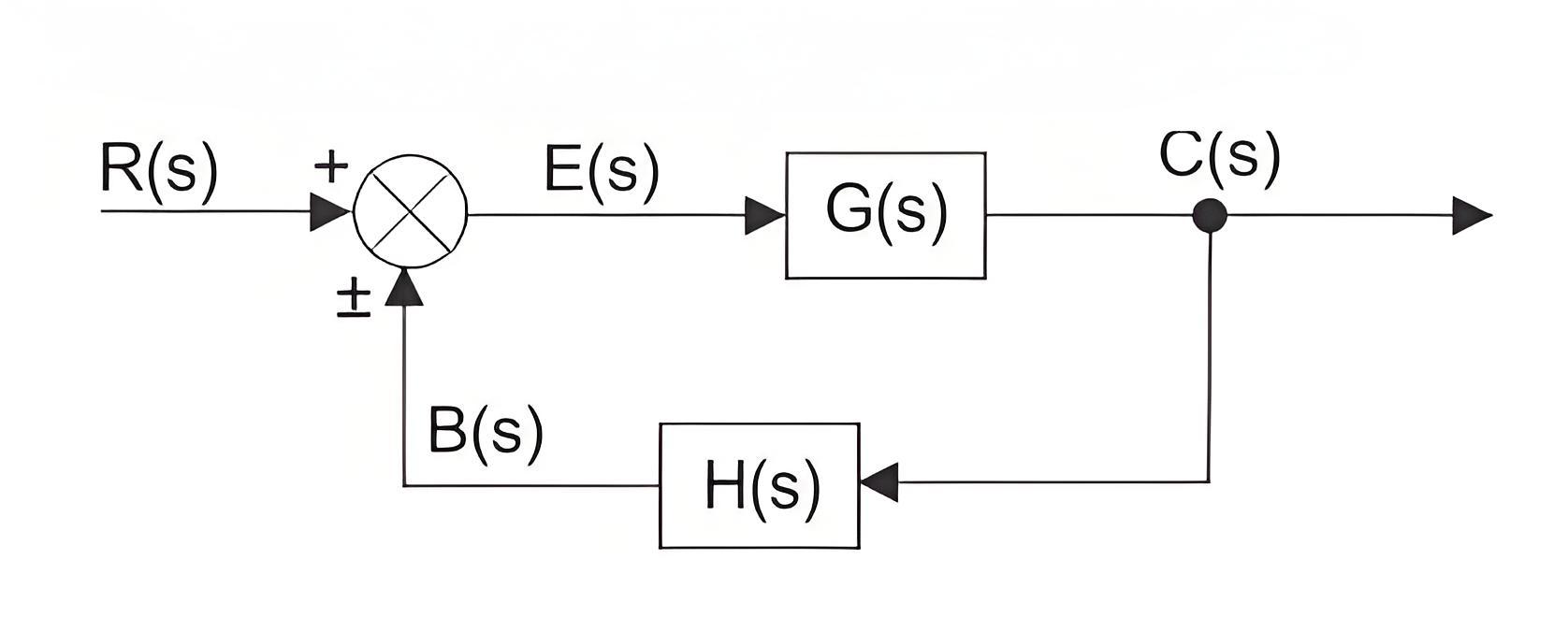
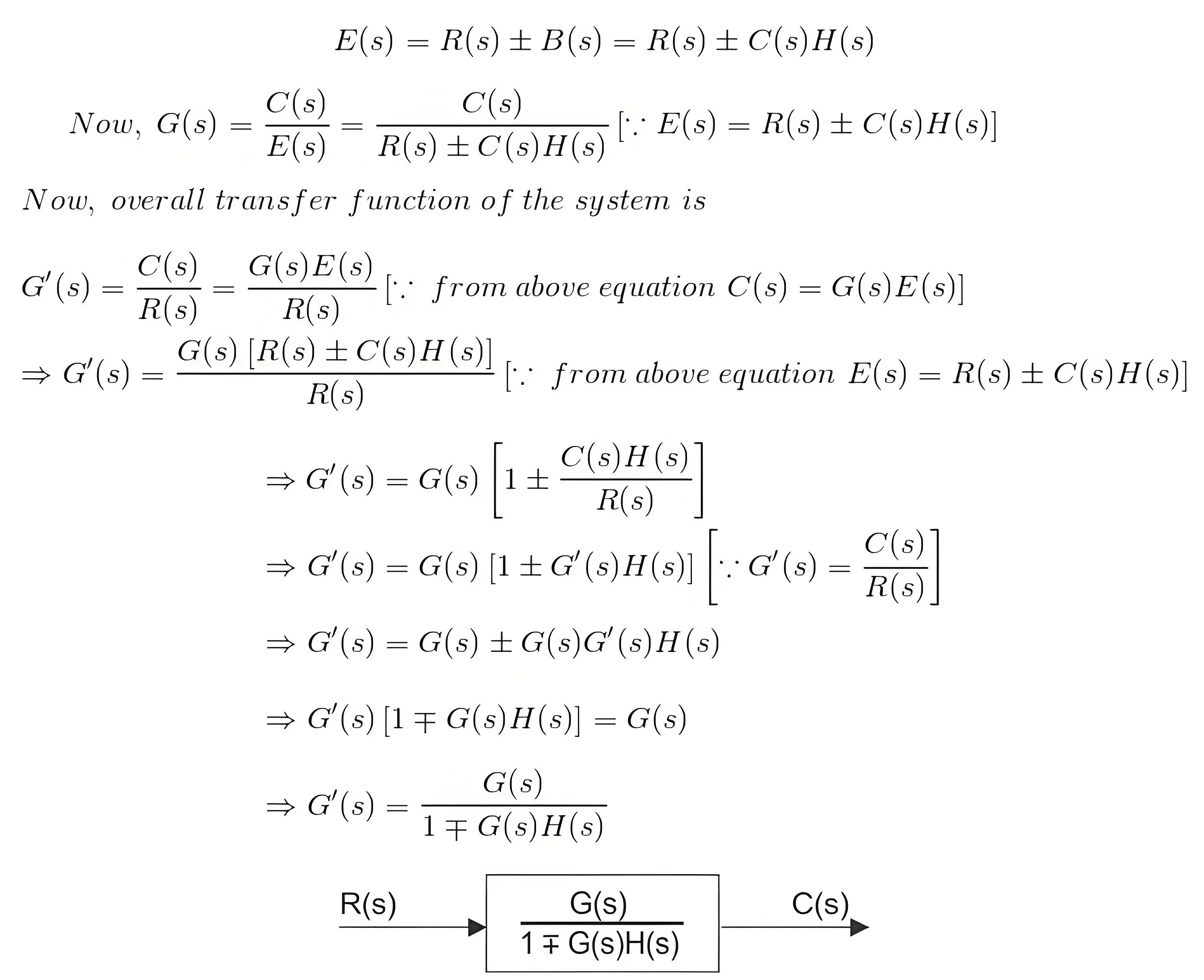
In a closed-loop control system, a fraction of output is fed-back and added to the system’s input. If H (s) is the transfer function of the feedback path, then the transfer function of the feedback signal will be B(s) = C(s)H(s).
At the summing point, the input signal R(s) will be added to B(s) and produces the actual input signal or error signal of the system, and it is denoted by E(s).
The Electricity Encyclopedia is dedicated to accelerating the dissemination and application of electricity knowledge and adding impetus to the development and innovation of the electricity industry.