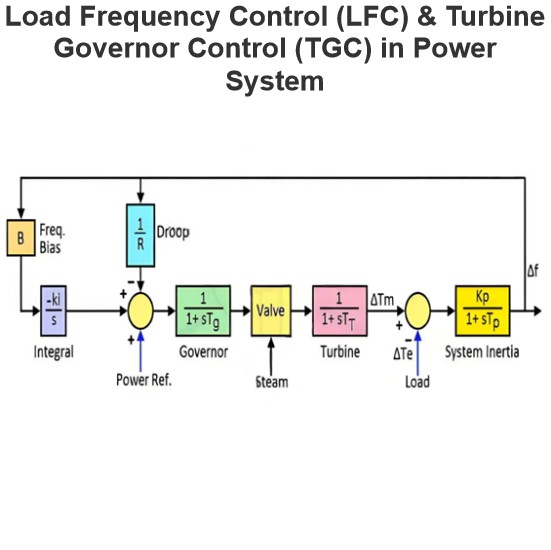
How do you prove that active power is the one responsible for mechanical work and not reactive power?
How to Prove that Active Power is the Power that Generates Mechanical Work, Not Reactive Power
To prove that active power (Active Power, P) is the power that generates mechanical work, rather than reactive power (Reactive Power, Q), we can examine the physical principles of power systems and the nature of energy conversion. Below is a detailed explanation:
1. Definitions of Active Power and Reactive Power
Active Power P: Active power refers to the actual electrical power consumed in an AC circuit that is converted into useful work. It is associated with resistive elements and represents the conversion of electrical energy into other forms of energy, such as thermal or mechanical energy. The unit of active power is watts (W).
Reactive Power Q: Reactive power refers to the portion of electrical power in an AC circuit that oscillates between the source and the load due to the presence of inductive or capacitive elements. It does not directly perform useful work but affects the voltage and current distribution in the system, impacting its efficiency. The unit of reactive power is volt-amperes reactive (VAR).
2. Power Factor and Phase Difference
In an AC circuit, the phase difference between the current and voltage determines the ratio of active power to reactive power. The power factor cos(ϕ) is a measure of this phase difference, where ϕ is the phase angle between the current and voltage.
When ϕ=0 , the current and voltage are in phase, and only active power exists, with no reactive power. This is common in purely resistive loads.
When ϕ=0 , the current and voltage are out of phase, resulting in both active and reactive power. For inductive loads (such as motors), the current lags behind the voltage; for capacitive loads, the current leads the voltage.
3. Energy Conversion Perspective
Physical Meaning of Active Power:
Active power is the power that, through resistive elements, converts electrical energy into other forms of energy, such as mechanical energy or heat. For example, in a motor, active power overcomes the load resistance, driving the rotor to rotate and produce mechanical work.
The magnitude of active power determines the actual energy consumption in the system, making it the power directly related to performing useful work.
Physical Meaning of Reactive Power:
Reactive power does not directly perform useful work but is associated with the storage of energy in magnetic or electric fields within inductive or capacitive elements. It oscillates between the source and the load without producing net mechanical work.
The primary role of reactive power is to maintain the voltage levels in the circuit and support the establishment and maintenance of magnetic or electric fields. Although it does not directly do work, it is necessary for the stable operation of the system.
4. Example with an Electric Motor
Using an electric motor as an example, the distinction between active power and reactive power becomes clearer:
Active Power: The active power in a motor is used to overcome the load resistance, driving the rotor to rotate and generate mechanical work. This part of the power ultimately converts into mechanical energy, powering machinery such as pumps or fans.
Reactive Power: The reactive power in a motor is used to establish and maintain the magnetic field between the rotor and stator. This magnetic field is essential for the motor's operation, but it does not directly produce mechanical work. Reactive power oscillates between the power source and the motor, not converting into useful mechanical energy.
5. Law of Conservation of Energy
According to the law of conservation of energy, the electrical energy input to a system must equal the output energy (including mechanical and thermal energy) plus any losses (such as resistive losses). Active power is the portion of electrical energy that is actually consumed and converted into useful work, while reactive power is temporarily stored in magnetic or electric fields and does not directly contribute to useful work.
6. Mathematical Expression
In a three-phase AC circuit, the total apparent power S (Apparent Power) can be expressed as:
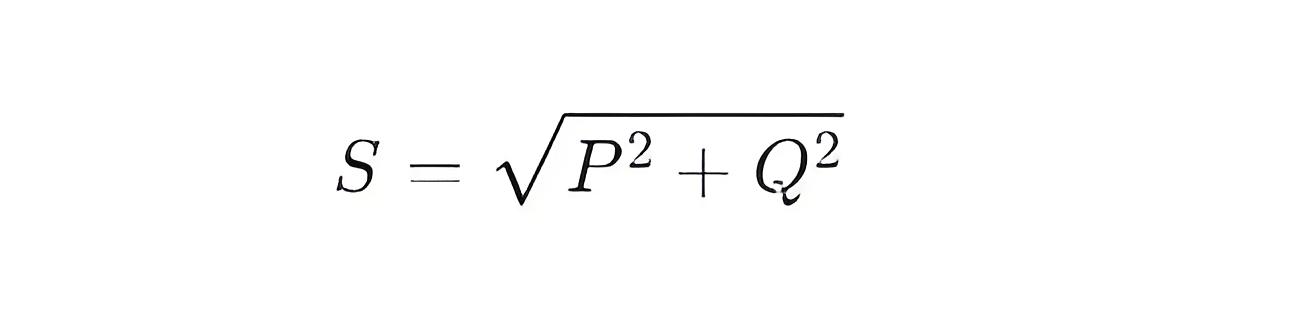
Where:
P is the active power, measured in watts (W).
Q is the reactive power, measured in volt-amperes reactive (VAR).
Active power P can be calculated using the following formula:
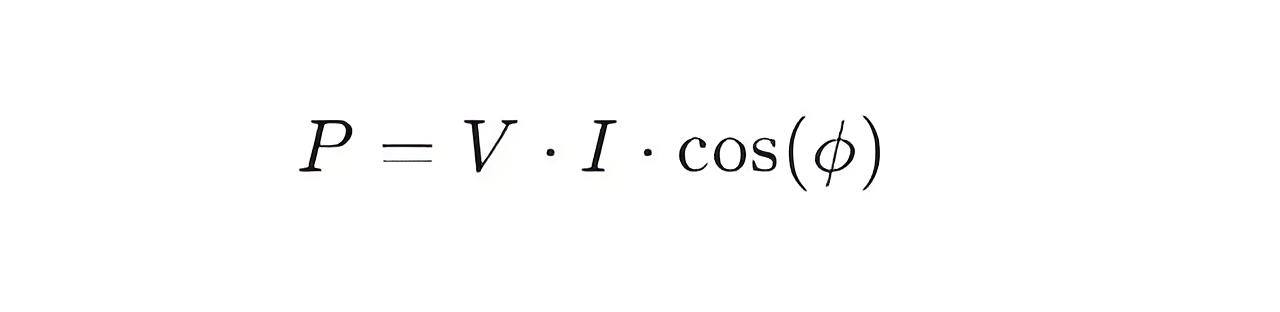
Reactive power Q can be calculated using the following formula:
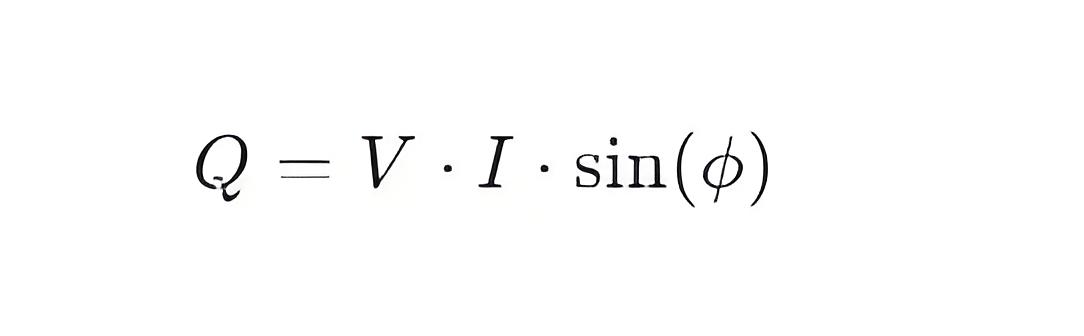
Here, V is the line voltage, I is the line current, and ϕ is the phase angle between the current and voltage.
7. Summary
Active Power is the actual power consumed and converted into useful work, such as mechanical or thermal energy. It is associated with resistive elements and can generate mechanical work.
Reactive Power is the power associated with inductive or capacitive elements, oscillating between the source and the load. It maintains magnetic or electric fields but does not directly perform useful work.
Therefore, active power is the power that generates mechanical work, while reactive power, although crucial for system stability, does not directly contribute to performing work. Reactive power supports the energy transfer process by maintaining the necessary magnetic or electric fields.
The Electricity Encyclopedia is dedicated to accelerating the dissemination and application of electricity knowledge and adding impetus to the development and innovation of the electricity industry.